题目内容
【题目】如图,已知一次函数![]() 的图像与
的图像与![]() 轴交于点
轴交于点![]() ,一次函数
,一次函数![]() 的图像与
的图像与![]() 轴交于点
轴交于点![]() ,且与
,且与![]() 轴以及一次函数
轴以及一次函数![]() 的图像分别交于点
的图像分别交于点![]() 、
、![]() ,点
,点![]() 的坐标为
的坐标为![]() .
.

(1)关于![]() 、
、![]() 的方程组
的方程组![]() 的解为______________.
的解为______________.
(2)关于![]() 的不等式
的不等式![]() 的解集为__________________.
的解集为__________________.
(3)求四边形![]() 的面积;
的面积;
(4)在![]() 轴上是否存在点
轴上是否存在点![]() ,使得以点
,使得以点![]() ,
,![]() ,
,![]() 为顶点的三角形是直角三角形?若存在,求出点
为顶点的三角形是直角三角形?若存在,求出点![]() 的坐标:若不存在,请说明理由.
的坐标:若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)4;(4)点
;(3)4;(4)点![]() 坐标为
坐标为![]() 或
或![]() .
.
【解析】
(1)把D(-2,m)代入y=x-2可得D的坐标.由图象可得结论;
(2)观察图象可得结论;
(3)过点D作DH⊥AB于H.根据S四边形OADC=SΔABD-SΔOBC计算即可;
(4)分三种情况讨论:①当点E为直角顶点时,过点D作DE1⊥x轴于E1,即可得出结论;
②当点C为直角顶点时,x轴上不存在点E;③当点D为直角顶点时,过点D作DE2⊥CD交x轴于点E2.设E2(t,0),利用勾股定理即可得出结论.
(1)∵D(-2,m)在y=x-2上,
∴m=-2-2=-4,
∴D(-2,-4).
由图象可知:关于x、y的方程组![]() 的解为
的解为![]() ;
;
(2)由图象可知:关于x的不等式x-2≥4x+b的解集为x≤-2;
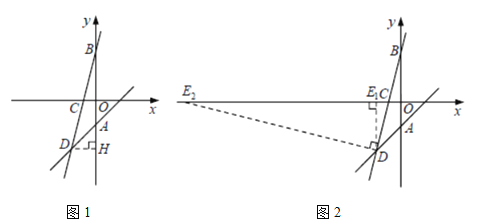
(3)如图1,过点D作DH⊥AB于H.
由(1)知D(-2,-4),
∴DH=2.
在y=x-2中,当x=0时,y=-2,
∴A(0,-2).
把D(-2,-4)代入y=4x+b得:-4=4×(-2)+b,解得:b=4.
∴B(0,4),
∴直线BD的函数表达式为y=4x+4.
∴AB=4-(-2)=6,
∴SΔABD=![]() ABDH=
ABDH=![]() ×6×2=6.
×6×2=6.
在y=4x+4中,当y=0时,0=4x+4,解得:x=-1.
∴C(-1,0),
∴OC=1.
∵B(0,4),
∴OB=4,
∴SΔOBC=![]() OBOC=
OBOC=![]() ×4×1=2,
×4×1=2,
∴S四边形OADC=SΔABD-SΔOBC=6-2=4.
(4)如图2,①当点E为直角顶点时,过点D作DE
∵D(-2,-4),
∴E1(-2,0)
②当点C为直角顶点时,x轴上不存在点E.
③当点D为直角顶点时,过点D作DE2⊥CD交x轴于点E2.设E2(t,0).
∵C(-1,0),E1(-2,0),
∴CE2=-1-t,E1E2=-2-t.
∵D(-2,-4),
∴DE1=4,CE1=-1-(-2)=1.
在![]() 中,由勾股定理得:
中,由勾股定理得:![]() .
.
在![]() 中,由勾股定理得:
中,由勾股定理得:![]() .
.
在![]() 中,由勾股定理得:
中,由勾股定理得:![]() .
.
∴(-1-t)2=t2+4t+20+17
解得:t=-18.
∴E2 (-18,0).
综合上所述:点E坐标为(-2,0)或(-18,0).

【题目】在初中阶段的函数学习中,我们经历了“确定函数的表达式——利用函数图象研究其性质——运用函数解决问题”的学习过程. 在画函数图象时,我们通过描点、平移、对称的方法画出了所学的函数图象. 同时,我们也学习了绝对值的意义![]() ,结合上面经历的学习过程,现在来解决下面的问题
,结合上面经历的学习过程,现在来解决下面的问题
在函数![]() 中,自变量
中,自变量![]() 的取值范围是全体实数,下表是
的取值范围是全体实数,下表是![]() 与
与![]() 的几组对应值:
的几组对应值:
|
| 0 | 1 | 2 | 3 | ||
y | … | 0 | 1 | 2 | 3 | 2 | … |
(1)根据表格填写:![]() _______.
_______.
(2)化简函数解析式:
当![]() 时,
时,![]() _______;
_______;
当![]() 时,
时,![]() ______.
______.
(3)在给出的平面直角坐标系中,请用你喜欢的方法画出这个函数的图象并解决以下问题;
①该函数的最大值为_______.
②若![]() 为该函数图象上不同的两点,则
为该函数图象上不同的两点,则![]() ________.
________.
③根据图象可得关于![]() 的方程
的方程![]() 的解为_______.
的解为_______.
【题目】如图,在![]() 中,
中,![]() 是
是![]() 的中点,
的中点,![]() 是边
是边![]() 上一动点,连结
上一动点,连结![]() ,取
,取![]() 的中点
的中点![]() ,连结
,连结![]() .小梦根据学习函数的经验,对
.小梦根据学习函数的经验,对![]() 的面积与
的面积与![]() 的长度之间的关系进行了探究:
的长度之间的关系进行了探究:

(1)设![]() 的长度为
的长度为![]() ,
,![]() 的面积
的面积![]() ,通过取
,通过取![]() 边上的不同位置的点
边上的不同位置的点![]() ,经分析和计算,得到了
,经分析和计算,得到了![]() 与
与![]() 的几组值,如下表:
的几组值,如下表:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 3 |
| 1 | 0 |
| 2 | 3 |
根据上表可知,![]() ______,
______,![]() ______.
______.
(2)在平面直角坐标系![]() 中,画出(1)中所确定的函数的图象.
中,画出(1)中所确定的函数的图象.

(3)在(1)的条件下,令![]() 的面积为
的面积为![]() .
.
①用![]() 的代数式表示
的代数式表示![]() .
.
②结合函数图象.解决问题:当![]() 时,
时,![]() 的取值范围为______.
的取值范围为______.





