题目内容
【题目】
是等边三角形，点
在射线
上，延长
至
，使
.
（1）如图（1），当点为线段中点时，求证：
.
（2）如图（2），当点在线段的延长线上时，还成立吗？若成立，请给予证明；若不成立，请说明理由.
【答案】（1）见解析；（2）
成立，证明见解析.
【解析】
（1）根据等边三角形的性质可得∠ABC=∠ACB=60°，由等腰三角形“三线合一”的性质可得∠CBD=30°，由CD=AD，CD=CE可得CD=CE，即可得∠CDE=∠CED，利用三角形外角性质可得∠CED=30°，可得∠CBD=∠CED，即可证明DB=DE；
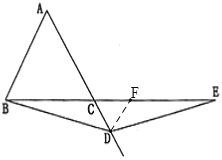
（2）如图，过点
作
的平行线
交
于
，根据平行线的性质及等边三角形的性质可证明△CDF是等边三角形，可得CD=DF=CF，利用线段的和差关系可得BC=AC=EF，利用平角的定义可得
=120°，利用SAS可证明
，即可得DB=DE.
（1）∵
是等边三角形
∴
∵点为线段
的中点，
∴
平分
，
∴
∵
∴
∴
∵
，
∴
，
，
∴∠CBD=∠CED，
∴；
（2）成立，理由如下：
如图，过点作的平行线交于，
∴
，
，
∵是等边三角形，
∴
，
，
∴
，
∵
，
∴
为等边三角形，
∴
，
∵，
∴
，
∴
，
∵
，
，
∴，
在
和
中，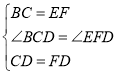
，
∴，
∴.
练习册系列答案
相关题目
