题目内容
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 在边
在边![]() 上,
上,![]() 在线段
在线段![]() 上,
上,![]() ,
,![]() 是等边三角形,边
是等边三角形,边![]() 交边
交边![]() 于点
于点![]() ,边
,边![]() 交边
交边![]() 于点
于点![]() .
.
![]() 求证:
求证:![]() ;
;
![]() 当
当![]() 为何值时,以
为何值时,以![]() 为圆心,以
为圆心,以![]() 为半径的圆与
为半径的圆与![]() 相切?
相切?
![]() 设
设![]() ,五边形
,五边形![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 之间的函数解析式(要求写出自变量
之间的函数解析式(要求写出自变量![]() 的取值范围);当
的取值范围);当![]() 为何值时,
为何值时,![]() 有最大值?并求
有最大值?并求![]() 的最大值.
的最大值.

【答案】![]() 证明见解析;
证明见解析;![]() 当
当![]() 时,以
时,以![]() 为圆心,以
为圆心,以![]() 为半径的圆与
为半径的圆与![]() 相切;
相切;![]() 当
当![]() 时,
时,![]() 有最大值,最大值为
有最大值,最大值为![]() .
.
【解析】
(1)由AB=AC,∠B=30°,根据等边对等角,可求得∠C=∠B=30°,又由△DEF是等边三角形,根据等边三角形的性质,易求得∠MDB=∠NEC=120°,∠BMD=∠B=∠C=∠CNE=30°,即可判定:△BMD∽△CNE;
(2)首先过点M作MH⊥BC,设BD=x,由以M为圆心,以MF为半径的圆与BC相切,可得MH=MF=4-x,由(1)可得MD=BD,然后在Rt△DMH中,利用正弦函数,即可求得答案;
(3)首先求得△ABC的面积,继而求得△BDM的面积,然后由相似三角形的性质,可求得△CNE的面积,再利用二次函数的最值问题,即可求得答案.
![]() ∵
∵![]() ,
,
∴![]() ,
,
∵![]() 是等边三角形,
是等边三角形,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
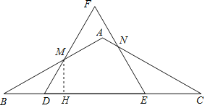
![]() 过点
过点![]() 作
作![]() ,
,
∵以![]() 为圆心,以
为圆心,以![]() 为半径的圆,则与
为半径的圆,则与![]() 相切,
相切,
∴![]() ,
,
设![]() ,
,
∵![]() 是等边三角形,
是等边三角形,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,
,
解得:![]() ,
,
∴当![]() 时,以
时,以![]() 为圆心,以
为圆心,以![]() 为半径的圆与
为半径的圆与![]() 相切;
相切;
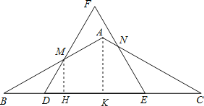
![]() 过点
过点![]() 作
作![]() 于
于![]() ,过点
,过点![]() 作
作![]() 于
于![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
由![]() 得:
得:![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() 是等边三角形且
是等边三角形且![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴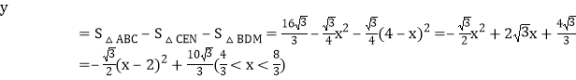 ,
,
当![]() 时,
时,![]() 有最大值,最大值为
有最大值,最大值为![]() .
.

练习册系列答案
相关题目







