��Ŀ����
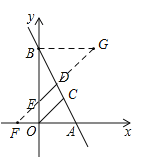
����Ŀ����ͼ1��ֱ��AB�ֱ���x�ᡢy�ύ��A��B���㣬OCƽ�֡�AOB��AB�ڵ�C����DΪ�߶�AB��һ�㣬����D��DE��OC��y���ڵ�E����֪AO��m��BO��n����m��n����n2��8n+16+|n��2m|��0��

��1����A��B��������ꣻ
��2������DΪAB�е㣬��OE�ij���
��3����ͼ2������P��x����2x+4��Ϊֱ��AB��x���·���һ�㣬��E��y�����������һ���㣬��EΪֱ�Ƕ���������ֱ����PEF��ʹ��F�ڵ�һ���ޣ���F��ĺᡢ������ʼ����ȣ����P�����꣮
���𰸡���1����AΪ��2��0������BΪ��0��4������2��OE��1����3����PΪ��4����4��
��������
��1�����ݷǸ��������ʣ��ó����̣�n��4��2+|n��2m|��0�����m��2��n��4�����ɵõ�A��B��������ꣻ
��2���ӳ�DE��x���ڵ�F���ӳ�FD����G��ʹ��DG��DF������BG������ȫ�������Σ��ٸ���BG=BE=AF�г�����x�ķ��̣��������OE�ij���
��3���ֱ����F��P��FM��y���ڵ�M��PN��y���ڵ�N�����EΪ��0��m��������ȫ�������Σ��ٸ���F��ĺ���������������ȣ��ó�����m+2x��4��m+x����ã�x=4�����ɵõ���PΪ��4��-4����
�⣺��1����n2��8n+16+|n��2m|��0��
�ࣨn��4��2+|n��2m|��0��
�ߣ�n��4��2��0��|n��2m|��0��
�ࣨn��4��2��0��|n��2m|��0��
��m��2��n��4��
���A��2��0������B��0��4����
��2���ӳ�DE��x���ڵ�F���ӳ�FD����G��ʹ��DG��DF������BG��
��OE��x��
��OCƽ�֡�AOB��
���BOC����AOC��45����
��DE��OC��
���EFO����FEO����BEG����BOC����AOC��45����
��OE��OF��x��
����ADF����BDG��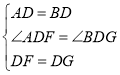 ��
��
���ADF�ա�BDG��SAS����
��BG��AF��2+x����G����AFE��45����
���G����BEG��45��
��BG��BE��4��x
��4��x��2+x��
��ã�x��1����OE��1��
��3���ֱ����F��P��FM��y���ڵ�M��PN��y���ڵ�N��
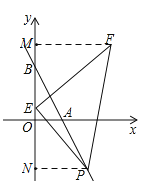
���E��0��m����
�ߵ�P������Ϊ��x����2x+4����
��PN��x��EN��m+2x��4��
�ߡ�PEF��90����
���PEN+��FEM��90����
��FM��y�ᣬ
���MFE+��FEM��90����
���PEN����MFE��
����EFM����PEN��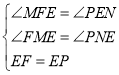 ��
��
���EFM�ա�PEN��AAS����
��ME��NP��x��FM��EN��m+2x��4��
���F��m+2x4��m+x����
��F��ĺ���������������ȣ�
��m+2x��4��m+x��
��ã�x��4��
���P��4����4����





