题目内容
【题目】一般情况下，中学生完成数学家庭作业时，注意力指数随时间x（分钟）的变化规律如图所示（其中AB、BC为线段，CD为双曲线的一部分）．
（1）分别求出线段AB和双曲线CD的函数关系式；
（2）若学生的注意力指数不低于40为高效时间，根据图中信息，求出一般情况下，完成一份数学家庭作业的高效时间是多少分钟？
【答案】（1）AB解析式为：y1=2x+30（0≤x≤10），曲线CD的解析式为：y2=
（x≥44）；（2）完成一份数学家庭作业的高效时间是50分钟
【解析】分析：(1)、利用待定系数法分别求出函数解析式；(2)、将y=40分别代入两个函数解析式分别求出x的值，然后进行做差得出答案．
详解：（1）设线段AB所在的直线的解析式为y1=k1x+30， 把B（10，50）代入得，k1=2，
∴AB解析式为：y1=2x+30（0≤x≤10）． 设C、D所在双曲线的解析式为y2=
，
把C（44，50）代入得，k2=2200， ∴曲线CD的解析式为：y2=
（x≥44）；
（2）将y=40代入y1=2x+30得：2x+30=40，解得：x=5，
将y=40代入y2=得：x=55． 55﹣5=50．
所以完成一份数学家庭作业的高效时间是50分钟．
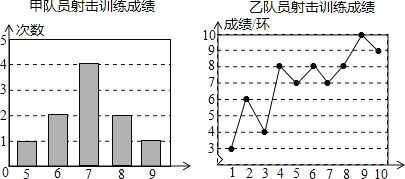
【题目】为了发展学生的核心素养，培养学生的综合能力，某中学利用“阳光大课间”，组织学生积极参加丰富多彩的课外活动，学校成立了舞蹈队、足球队、篮球队、毽子队、射击队等，其中射击队在某次训练中，甲、乙两名队员各射击10发子弹，成绩记录如表：
射击次序（次） | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
甲的成绩（环） | 8 | 9 | 7 | 9 | 8 | 6 | 7 | a | 10 | 8 |
乙的成绩（环） | 6 | 7 | 9 | 7 | 9 | 10 | 8 | 7 | 7 | 10 |
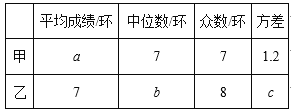
（1）经计算甲和乙的平均成绩是8（环），请求出表中的a＝ ；
（2）甲成绩的中位数是 环，乙成绩的众数是 环；
（3）若甲成绩的方差是1.2，请求出乙成绩的方差，判断甲、乙两人谁的成绩更为稳定？
