题目内容
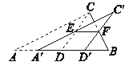
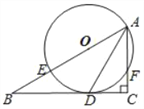
【题目】已知:如图, AF平分∠BAC,BC⊥AF, 垂足为E,点D与点A关于点E对称,PB分别与线段CF,AF相交于P,M.

(1)求证:AB=CD;
(2)若∠BAC=2∠MPC,请你判断∠F与∠MCD的数量关系,并说明理由.
【答案】(1)证明见解析;(2)∠F=∠MCD,理由见解析.
【解析】
(1)根据全等三角形的性质和判定和线段垂直平分线性质求出AB=AC=CD,
(2)由AB=AC=CD推出∠CDA=∠CAD=∠CPM,求出∠MPF=∠CDM,∠PMF=∠BMA=∠CMD,在△DCM和△PMF中根据三角形的内角和定理求出即可.
(1)∵AF平分∠BAC,BC⊥AF,
∴∠CAE=∠BAE,∠AEC=∠AEB=90°,
在△ACE和△ABE中,∵∠AEC=∠AEB,AE=AE,∠CAE=∠BAE,
∴△ACE≌△ABE(ASA),
∴AB=AC,
∵∠CAE=∠CDE,
∴AM是BC的垂直平分线,
∴CM=BM,CE=BE,
∴∠CMA=∠BMA,
∵AE=ED,CE⊥AD,
∴AC=CD,
∴AB=CD;
(2)∠F=∠MCD,
理由是:∵AC=CD,
∴∠CAD=∠CDA,
∵∠BAC=2∠MPC,
又∵∠BAC=2∠CAD,
∴∠MPC=∠CAD,
∴∠MPC=∠CDA,
∴∠MPF=∠CDM,
∴∠MPF=∠CDM(等角的补角相等),
∵∠DCM+∠CMD+∠CDM=180°,∠F+∠MPF+∠PMF=180°,
又∵∠PMF=∠BMA=∠CMD,
∴∠MCD=∠F.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】已知△ABC中∠ACB=90°,E在AB上,以AE为直径的⊙O与BC相切于D,与AC相交于F,连接AD.
(1)求证:AD平分∠BAC;
(2)连接OC,如果∠B=30°,CF=1,求OC的长.
【题目】一次期中考试中,甲、乙、丙、丁、戍五位同学的数学、英语成绩等有关信息如下 表所示:(单位:分)
甲 | 乙 | 丙 | 丁 | 戍 | 平均分 | 标准差 | |
数学 | 71 | 72 | 69 | 68 | 70 |
| |
英语 | 88 | 82 | 94 | 85 | 76 | 85 |
(1)求这五位同学在本次考试中数学成绩的平均分和英语成绩的标准差;
(2)为了比较不同学科考试成绩的好与差,采用标准分是一个合理的选择.标准分 的计算公式是:标准分=(个人成绩-平均成绩)÷成绩标准差.从标准分看, 标准分大的考试成绩更好.请问甲同学在本次考试中,数学与英语哪个学科考 得更好?