题目内容
【题目】甲、乙两名队员参加射击训练，成绩分别被制成下列两个统计图：
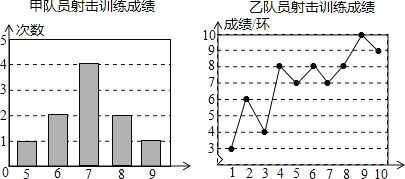
根据以上信息，整理分析数据如下：
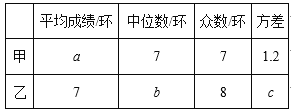
（1）写出表格中a，b，c的值：a＝ ，b＝ ，c＝ ．
（2）如果乙再射击一次，命中7环，那么乙的射击成绩的方差 ．（填“变大”“变小”“不变”）
（3）教练根据这10次成绩若选择甲参加比赛，教练的理由是什么？
【答案】（1）a＝7，b＝7.5，c＝4.2；（2）变小；（3）因为他们的平均数相同，而甲的方差小，发挥比较稳定，所以选择甲参加射击比赛
【解析】
（1）利用平均数的计算公式直接计算平均分即可；将乙的成绩从小到大重新排列，用中位数的定义直接写出中位数即可；根据乙的平均数利用方差的公式计算即可；
（2）如果乙再射击一次，命中7环，那么乙的射击成绩的平均数不变，求得方差即可得出结论；
（3）他们的平均数相同，而甲的方差小，发挥比较稳定，所以选择甲参加射击比赛．
解：（1）甲的平均成绩a＝
＝7（环），
甲的成绩的众数c＝7（环），
∵乙射击的成绩从小到大重新排列为：3、4、6、7、7、8、8、8、9、10，
∴乙射击成绩的中位数b＝
＝7.5（环），
其方差d＝
×[（3﹣7）2+（4﹣7）2+（6﹣7）2+2×（7﹣7）2+3×（8﹣7）2+（9﹣7）2+（10﹣7）2]
＝×（16+9+1+3+4+9）
＝4.2；
故答案为：7，7.5，4.2；
（2）如果乙再射击一次，命中7环，那么乙的射击成绩的平均数不变，方差为：
×[（3﹣7）2+（4﹣7）2+（6﹣7）2+2×（7﹣7）2+3×（8﹣7）2+（9﹣7）2+（10﹣7）2+（7﹣7）2]
＝×（16+9+1+3+4+9）
＝
＜4.2；
∴乙的射击成绩的方差变小，
故答案为：变小；
（3）因为他们的平均数相同，而甲的方差小，发挥比较稳定，所以选择甲参加射击比赛．
