题目内容
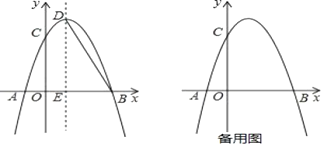
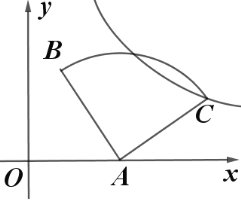
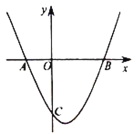
【题目】如图,在平面直角坐标系中,点![]() 为原点,直线
为原点,直线![]() (
(![]() 为常数,且
为常数,且![]() )经过点
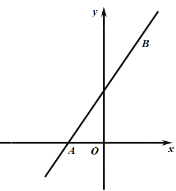
)经过点![]() ,交
,交![]() 轴于点
轴于点![]() ,已知点
,已知点![]() 的坐标为
的坐标为![]()
![]() 求
求![]() 的值;
的值;
![]() 过点
过点![]() 作
作![]() 轴,垂足为点
轴,垂足为点![]() ,点
,点![]() 在
在![]() 的延长线上,连接
的延长线上,连接![]() ,且
,且![]() 在线段
在线段![]() 上分别取点
上分别取点![]() 使得
使得![]() ,连接
,连接![]() ,设点
,设点![]() 的纵坐标为
的纵坐标为![]() ,
,![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 之间的函数关系式(不要求写出自变量
之间的函数关系式(不要求写出自变量![]() 的取值范围);
的取值范围);
![]() 在(2)的条件下,连接
在(2)的条件下,连接![]() ,当
,当![]() 时,点
时,点![]() 在线段
在线段![]() 上,连接
上,连接![]() 且
且![]() .求
.求![]() 的值.
的值.


【答案】![]() 3;
3;![]()
![]() ;
;![]()
![]()
【解析】
![]() 将点B的坐标代入解析式中即可求出结论;
将点B的坐标代入解析式中即可求出结论;
![]() 过点
过点![]() 作
作![]() 于点
于点![]() ,过点
,过点![]() 分别作
分别作![]() 于点
于点![]() 轴于点
轴于点![]() 的延长线交
的延长线交![]() 于点
于点![]() ,用含t的式子表示出BK,然后利用等角的锐角三角函数相等可得
,用含t的式子表示出BK,然后利用等角的锐角三角函数相等可得![]() ,从而求出AH,然后根据三角形的面积公式即可求出结论;
,从而求出AH,然后根据三角形的面积公式即可求出结论;
![]() 取
取![]() 的中点
的中点![]() ,连接
,连接![]() ,根据直角三角形的性质可得
,根据直角三角形的性质可得![]() ,设
,设![]() ,用a表示出各个角的大小,在
,用a表示出各个角的大小,在![]() 上取一点
上取一点![]() ,使
,使![]() ,连接
,连接![]() ,利用SAS证出
,利用SAS证出![]() ,利用勾股定理求出
,利用勾股定理求出![]() ,然后求出点A的坐标,代入解析式中即可求出结论.
,然后求出点A的坐标,代入解析式中即可求出结论.
解:![]() 点
点![]() 在直线
在直线![]() 上
上
![]()
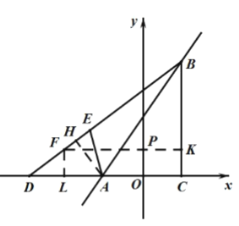
![]() 如图 1,过点
如图 1,过点![]() 作
作![]() 于点
于点![]() ,过点
,过点![]() 分别作
分别作![]() 于点
于点![]() 轴于点
轴于点![]() 的延长线交
的延长线交![]() 于点
于点![]()
![]()
![]() 四边形
四边形![]() 为矩形,
为矩形, ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
在![]() 中 ,
中 ,![]()
在![]() 中,
中,![]()
![]()
![]()
![]()
![]()
![]()
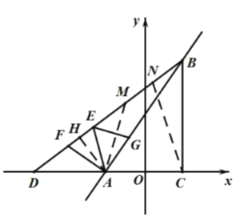
![]() 取
取![]() 的中点
的中点![]() ,连接
,连接![]()
![]()
![]()
![]()
![]()
![]()
![]()
设![]() ,则
,则![]()
![]()
在![]() 上取一点
上取一点![]() ,使
,使![]() ,连接
,连接![]()
又![]()
![]()
![]()
![]()
![]()
![]() 令
令![]() ,
,
则![]()
![]()
在![]() 中,
中,![]()
![]()
解得![]() (舍)
(舍)
![]()
![]()
![]()
设![]() ,则
,则![]()
![]() ,
,![]()
![]()
![]()
解得![]()
![]()
![]()
![]()
![]()
解得![]()

练习册系列答案
相关题目
【题目】为了迎接体育理化加试,九(2)班同学到某体育用品商店采购训练用球,已知购买3个A品牌足球和2个B品牌足球需付210元;购买2个A品牌足球和1个B品牌足球需付费130元.(优惠措施见海报)巨惠来袭(解释权归本店所有)
A品牌 | B品牌 |
|
|
单品数量低于40个不优惠,高于40个 享8折优惠 | 单品数量低于40个不优惠,高于40个 享9折优惠 |
(1)求A,B两品牌足球的单价各为多少元?
(2)为享受优惠,同学们决定购买一次性购买足球60个,若要求A品牌足球的数量不低于B品牌足球数量的3倍,请你设计一种付费最少的方案,并说明理由.