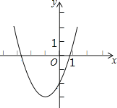题目内容
【题目】如图,在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,点
两点,点![]() 的坐标为
的坐标为![]() .
.
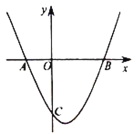
(1)求![]() 点坐标;
点坐标;
(2)若对于每一个给定的![]() 的值,它所对应的函数值都不小于
的值,它所对应的函数值都不小于![]() ,求
,求![]() 的取值范围.
的取值范围.
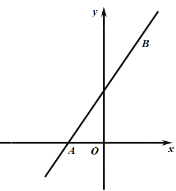
(3)直线![]() 经过点
经过点![]() .
.
①求直线和抛物线的解析式;
②设抛物线与![]() 轴的交点为
轴的交点为![]() ,过点
,过点![]() 作直线
作直线![]() 轴,将抛物线在
轴,将抛物线在![]() 轴左侧的部分沿直线
轴左侧的部分沿直线![]() 翻折,抛物线的其余部分保持不变,得到一个新图像,请你结合新图像回答:
翻折,抛物线的其余部分保持不变,得到一个新图像,请你结合新图像回答:
当直线![]() 与新图像只有一个公共点
与新图像只有一个公共点![]() 且
且![]() 时,求
时,求![]() 的取值范围.
的取值范围.
【答案】(1)点B的坐标为(4,0);(2)0<m≤![]() ;(3)①直线的解析式为y=
;(3)①直线的解析式为y=![]() x-2;②b的取值范围为-4<b≤5或b<-
x-2;②b的取值范围为-4<b≤5或b<-![]() .
.
【解析】
(1)由抛物线的解析式可知它的对称轴是x=1,从而可得答案;
(2)由题意得到抛物线的开口方向,结合抛物线的顶点坐标可得答案;
(3)①利用已知条件建立关于![]() 的方程组,从而可得答案;
的方程组,从而可得答案;
②求解![]() 过抛物线上纵坐标为
过抛物线上纵坐标为![]() 的点时,
的点时,![]() 的值,再判断
的值,再判断![]() (b<-4)与函数 y=
(b<-4)与函数 y=![]() x2-x-4(x>0)的图像仅有一个公共点P时,
x2-x-4(x>0)的图像仅有一个公共点P时,![]() 的值,结合图像可得答案.
的值,结合图像可得答案.
解:(1)依题意,可得抛物线的对称轴为:x=1.
∵抛物线与x轴交于A、B两点,点A的坐标为(-2,0),
∴点B的坐标为(4,0).
(2)∵点A在二次函数y=mx2-2mx+n的图像上,
∴0=4m+4m+n.即n=-8m.
∴y=mx2-2mx-8m=![]() ,顶点坐标是(1,-9m)
,顶点坐标是(1,-9m)
∵若对于每一个给定的x的值,它所对应的函数值都不小于-5,
∴![]()
即0<m≤![]() .
.
(3)①∵点B在直线y=![]() x+4m+n上,∴0=2+4m+n.
x+4m+n上,∴0=2+4m+n.
又 n=-8m,
∴m=![]() ,n=-4.
,n=-4.
抛物线的解析式为y=![]() x2-x-4,
x2-x-4,
直线的解析式为y=![]() x-2.
x-2.
②由y=![]() x2-x-4得:抛物线与y轴的交点为C(0,-4).
x2-x-4得:抛物线与y轴的交点为C(0,-4).
直线l:y=-4,依题意翻折后的图像如图所示.
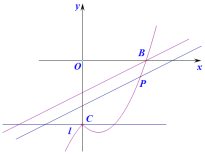
令y=8,则 ![]() x2-x-4=8.解得x1=-4,x2=6.
x2-x-4=8.解得x1=-4,x2=6.
∴新图像经过点(6,8).
当直线y=![]() x+b经过(6,8)点时,可得b=5.
x+b经过(6,8)点时,可得b=5.
当直线y=![]() x+b经过C点时,可得b=-4.
x+b经过C点时,可得b=-4.
当直线y=![]() x+b(b<-4)与函数 y=
x+b(b<-4)与函数 y=![]() x2-x-4(x>0)的图像仅有一个公共点P时,
x2-x-4(x>0)的图像仅有一个公共点P时,
也就是方程![]() x2-x-4=
x2-x-4=![]() x+b有相等的实数根.
x+b有相等的实数根.
整理方程,得 x2-3x-(8+2b)=0.
由根的判别式=(-3)2+4(8+2b)=8b+41=0,得b=-![]() .
.
结合图像可知,b的取值范围为-4<b≤5或b<-![]() .
.
【点晴】
本题考查的二次函数的基本性质,以及用待定系数法求函数的解析式,同时考查了函数只有一个交点时,字母的取值范围,从图像中获取信息就是解题的关键.