Question

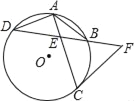
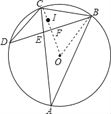
【题目】如图，已知△BAC为圆O内接三角形，AB＝AC，D为⊙O上一点，连接CD、BD，BD与AC交于点E，且BC2＝ACCE

①求证：∠CDB＝∠CBD；

②若∠D＝30°，且⊙O的半径为3+，I为△BCD内心，求OI的长．

Answer 1

【答案】①证明见解析；②.

【解析】

①先求出，然后求出△BCE和△ACB相似，根据相似三角形对应角相等可得∠A＝∠CBE，再根据在同圆或等圆中，同弧所对的圆周角相等可得∠A＝∠CDB，然后求出∠CDB＝∠CBD；

②连接OB、OC，根据在同圆或等圆中，同弧所对的圆心角等于圆周角的2倍求出∠BOC＝60°，然后判定△OBC是等边三角形，再根据等腰三角形三线合一的性质以及三角形的内心的性质可得OC经过点I，设OC与BD相交于点F，然后求出CF，再根据I是三角形的内心，利用三角形的面积求出IF，然后求出CI，最后根据OI＝OC﹣CI计算即可得解．

①证明：∵BC2＝ACCE，

∴，

∠BCE＝∠ACB，

∴△BCE∽△ACB，

∴∠CBD＝∠A，

∵∠A＝∠CDB，

∴∠CDB＝∠CBD．

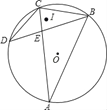
②解：连接OB、OC，

∵∠A＝∠D＝30°，

∴∠BOC＝2∠A＝2×30°＝60°，

∵OB＝OC，

∴△OBC是等边三角形，

∵CD＝CB，I是△BCD的内心，

∴OC经过点I，

设OC与BD相交于点F，

则CF＝BC×sin30°＝BC，

BF＝BCcos30°＝BC，

所以，BD＝2BF＝2×BC＝BC，

设△BCD内切圆的半径为r，

则S△BCD＝BDCF＝（BD+CD+BC）r，

即BCBC＝（BC+BC+BC）r，

解得r＝BC＝BC，

即IF＝BC，

所以，CI＝CF﹣IF＝BC﹣BC＝（2﹣）BC，

OI＝OC﹣CI＝BC﹣（2﹣）BC＝（﹣1）BC，

∵⊙O的半径为3+，

∴BC＝3+，

∴OI＝（﹣1）（3+）＝3+3﹣3﹣＝2．