Question

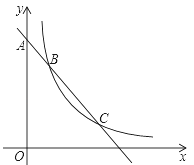
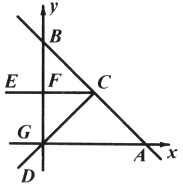
【题目】如图，在平面直角坐标系中，直线与轴交于点，与轴交于点，点是的中点，绕点按顺时针旋转，且，的一边交轴于点，开始时另一边经过点，点坐标为，当旋转过程中，射线与轴的交点由点到点的过程中，则经过点三点的圆的圆心所经过的路径长为（ ）

A. B. C. D.

Answer 1

【答案】A

【解析】

此题属于半角型题目.由题意得，圆心始终在线段BC的垂直平分线上，可证△BFC是直角三角形，所以一开始经过点三点的圆的圆心在BC的中点N.开始在BC的中点N处，当射线CD经过点G时，如图，此时圆心是F′B的垂直平分线与BC的垂直平分线的交点I,在 旋转过程中，射线与轴的交点由点到点的过程中，经过点三点的圆的圆心所经过的路径长为线段NI的长.

如图：旋转到射线经过点时，表示为∠E′CD′，F′B的垂直平分线MI与BC的垂直平分线NI交于点I, MI与BN交于点 H′.

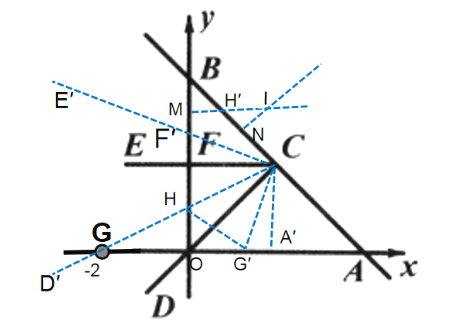
由题意得，A（4,0），B（0,4），AB的中点C（2,2），

∴∠COF=45°，又∵∠OCE=45°，∴∠CFO=90°，

过点C作CA′⊥x轴于点A′，即四边形A′OFC是边长为2的正方形.

在A′O上截取A′G′=FF′，易证Rt△CA′G′≌Rt△CFF′,

∴CF′=C G′,∠A′CG′=∠FCF′,即∠F′CG′=90°.

设A′G′=FF′=x，则O G′=2-x，F′H=H G′=x+1.

Rt△OHG′中，∵OH2+ O G′2= H G′2，即12+（2-x）2=(x+1)2,

解得：x= .

∴F′B=4-2-=.MB= F′B ==MH′，

在等腰直角三角形BM H′和等腰直角三角形 H′NI中，B H′= ，

∵BN=AB=×4=，

∴NI=H′N=BN-B H′=- =.

故选：A.