题目内容
【题目】如图,在△ABC中,∠ABC![]() 15°,AB
15°,AB![]()
![]() ,BC
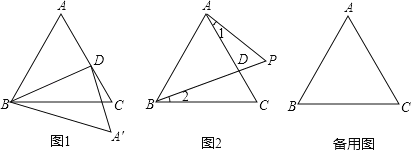
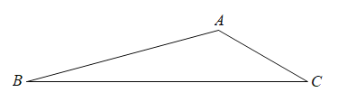
,BC![]() 2,以AB为直角边向外作等腰直角△BAD,且∠BAD=90°;以BC为斜边向外作等腰直角△BEC,连接DE.
2,以AB为直角边向外作等腰直角△BAD,且∠BAD=90°;以BC为斜边向外作等腰直角△BEC,连接DE.
(1)按要求补全图形;
(2)求DE长;
(3)直接写出△ABC的面积.
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]()
【解析】
(1)根据题意描述绘图即可.
(2)连接DC,先证明△BCD是等边三角形,再证明DE垂直平分BC.由勾股定理求出DF和EF的长度,DE=DF+EF.
(3)可以证明△ABC≌△DAC,用△DBC的面积减去△ABD的面积除以2即可得到△ABC的面积.
解:(1)如图所示
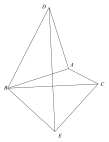
(2) 连接DC
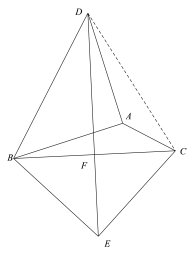
解:∵△ABD是等腰直角三角形, AB=![]() ,∠BAD=90°.
,∠BAD=90°.
∴ AB=AD=![]() ,∠ABD=45°.
,∠ABD=45°.
由勾股定理得DB=2.
∴ ∠DBC=∠ABC+∠ABD=60°.
∵BC=2.
∴ BC=BD.
∴△BCD是等边三角形.
∴BD=CD=2.
∴D点在线段BC的垂直平分线上.
又∵△BEC是等腰直角三角形.
∴BE=CE ,∠CEB=45°
∴E点在线段BC的垂直平分线上.
∴DE垂直平分BC.
∴BF=![]() BC=1, ∠BFE=90°
BC=1, ∠BFE=90°
∵∠FBE=∠BEF=45°
∴BF=EF=1
Rt△BFD中,BF=1,BD=2
由勾股定理得DF=![]() ,
,
∴ DE=DF+EF =![]() .
.
(3)∵AD=AB,DC=BC,AC=AC,
∴△ABC≌△DAC.
用△DBC的面积减去△ABD的面积除以2即可得到△ABC的面积.
△DBC的面积为![]() =
=![]() ,△ABD的面积为
,△ABD的面积为![]() .
.
所以△ABC的面积为![]() .
.

 备战中考寒假系列答案
备战中考寒假系列答案【题目】某体育用品商店一共购进20个篮球和排球,进价和售价如下表所示,全部销售完后共获得利润260元;
篮球 | 排球 | |
进价(元/个) | 80 | 50 |
售价(元/个) | 95 | 60 |
(1)列方程组求解:商店购进篮球和排球各多少个?
(2)销售6个排球的利润与销售几个篮球的利润相等?