��Ŀ����
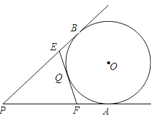
����Ŀ����ͼ1����ABC�ǵȱ������Σ���D��AC���϶��㣬��CBD����������ABD��BD���ۣ�A��Ӧ��ΪA'��
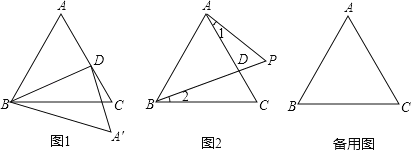
��1���ٵ�����15��ʱ����CBA'���� ����
��������ʾ��CBA'Ϊ�� ����
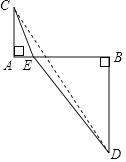
��2����ͼ2����P��BD�ӳ����ϣ��ҡ�1����2������
�ٵ�0��������60��ʱ����̽��AP��BP��CP֮���Ƿ����һ��������ϵ�����벢˵�����ɣ�
��BP��8��CP��n����CA'���� �������ú�n��ʽ�ӱ�ʾ��
���𰸡���1����30������60����2������2����BP��AP+CP�����ɼ���������8��2n
��������
��1���������ABC��60�����ó���ABD��60�������������۵��ó���A'BD��60�����������ɵó����ۣ�
��2�������жϳ���BP'C�ա�APC���ó�CP'��CP����BCP'����ACP�����жϳ���CPP'�ǵȱ������Σ��ó�PP'��CP��
���������BCP��120���������������BCA'��60��+�����жϳ���A'��C��P��ͬһ��ֱ���ϣ�����PA'��PC+CA'�����жϳ���ADP�ա�A'DP(SAS)���ó�A'P��AP�����ɵó����ۣ�
�⣺��1���ߡ�ABC�ǵȱ������Σ�
���ABC��60����
�ߡ�CBD������
���ABD����ABC����CBD��60��������
���۵�֪����A'BD����ABD��60��������
���CBA'����A'BD����CBD��60������������60����2����
�ٵ�����15��ʱ����CBA'��60����2����30����
�ʴ�Ϊ30����
��������ʾ��CBA'Ϊ60����2����
�ʴ�Ϊ60����2����
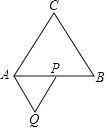
��2����BP��AP+CP�����ɣ���ͼ2������CP��

��BP��ȡһ��P'��ʹBP'��AP��
�ߡ�ABC�ǵȱ������Σ�
���ACB��60����BC��AC��
�ߡ�1����2������
���BP'C�ա�APC(SAS)��
��CP'��CP����BCP'����ACP��
���PCP'����ACP+��ACP'����BCP'+��ACP'����ACB��60����
��CP'��CP��
���CPP'�ǵȱ������Σ�
���CPB��60����PP'��CP��
��BP��BP'+PP'��AP+CP��
����ͼ3��
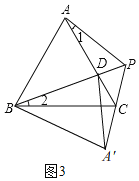
�ɢ�֪����BPC��60����
���BCP��180������BPC����PBC��180����60��������120��������
�ɣ�1��֪����CBA'��60����2����
���۵�֪��BA��BA'��
��BA��BC��
��BA'��BC��
���BCA'��![]() (180������CBA')��
(180������CBA')��![]() [180����(60����2��)]��60��+����
[180����(60����2��)]��60��+����
���BCP+��BCA'��120������+60��+����180����
���A'��C��P��ͬһ��ֱ���ϣ�
����PA'��PC+CA'��
���۵�֪��BA��BA'����ADB����A'DB��
��180������ADB��180������A'DB��
���ADP����A'DP��
��DP��DP��
���ADP�ա�A'DP(SAS)��
��A'P��AP��
�ɢ�֪��BP��AP+CP��
��BP��8��CP��n��
��AP��BP��CP��8��n��
��A'P��8��n��
��CA'��A'P��CP��8��n��n��8��2n��
�ʴ�Ϊ��8��2n��

 ���ɶ���ܲ��¿�ֱͨ�п�ϵ�д�
���ɶ���ܲ��¿�ֱͨ�п�ϵ�д�