题目内容
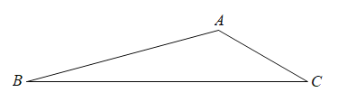
【题目】如图，在
中，已知
，
，求中各角的度数．
【答案】∠B＝∠C＝36°，∠CAB＝108°
【解析】
由AB=AC，AC=CD，BD=AD得∠B＝∠C＝∠BAD,∠CAD＝∠CDA, 设∠B＝x，由外角性质可得：∠CDA＝∠BAD+∠B=2x，根据三角形的内角和定理即可求得∠x的值，从而不难求得
中各角的度数．
解：∵AB=AC，AC=CD，BD=AD，
∴∠B＝∠C＝∠BAD,∠CAD＝∠CDA，（等边对等角）
设∠B＝x，则∠CDA＝∠BAD+∠B＝2x，
从而∠CAD＝∠CDA＝2x，∠C＝x
∴△ADC中，∠CAD+∠CDA+∠C＝2x+2x+x=180°
解得x= 36°
∴在△ABC中，∠B＝∠C＝36°，∠CAB＝108°
练习册系列答案
名校课堂系列答案
相关题目
