题目内容
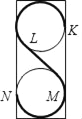
【题目】如图，字母S由两条圆弧KL、MN和线段LM组成，这两条圆弧每一条都是一个半径为1的圆的圆周的
，线段LM与两个圆相切．K和N分别是两个圆的切点，则线段LM的长为_________．
【答案】2
【解析】
连接O
L,OK, O
M , OO交LM于O,则∠LOK=(1-
)
360
=135,
由切线的性质可知∠KOO=90,可得∠L OO =45,又由切线的性质可知∠OLO=90,故△OLO为等腰直角三角形,LO=OL=1,同理可得OM=1,可求线段LM的长.
解:如图,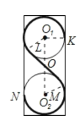 
连接OL,OK,OM,OO交LM于O,
依题意,得
∠LOK=(1-)360=135,
O,O为等圆,K为切点,
∠KOO=90,
∠L OO=∠LOK-∠KO0=135-90=45
∠M与O相切于点L, ∠OLO=90,
△OL0为等腰直角三角形,LO= OL=1,同理可得OM=1,
LM=LO+OM=2.
故答案为:2.
练习册系列答案
口算小状元口算速算天天练系列答案
相关题目
