题目内容
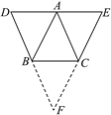
【题目】如图所示,已知BD∥AC,CE∥BA,且点D,A,E在一条直线上,设∠BAC=x,∠D+∠E=y.
(1)试用含x的代数式表示y;
(2)当x=90°时,判断直线DB与直线EC的位置关系,并说明理由.

【答案】(1)y=180°-x(0°<x<180°);(2)DB⊥EC.理由见解析.
【解析】
(1)根据两直线平行,同位角相等可得∠EAC =∠D,∠DAB =∠E,再根据平角等于180°列式整理即可得解;
(2)延长DB,EC交于点F,由BD∥AC,推出∠BAC=∠DBA.因为x=90°所以∠DBA=90°结合CE∥BA,可证DB⊥EC.
(1)y=180°-x(0°<x<180°).
(∵BD∥AC,CE∥BA,
∴∠EAC=∠D,∠DAB=∠E,
∵D、A.E在同一条直线上,
∴∠EAC +∠BAC+∠DAB =180°,
∵∠BAC=x,∠D+∠E=y,
∴x+y=180°,
∴y=180°x.)
(2)DB⊥EC.理由:如图,延长DB,EC交于点F.
∵BD∥AC,
∴∠BAC=∠DBA.
∵x=90°,即∠BAC=90°,
∴∠DBA=90°.
∵CE∥BA,
∴∠DFE=∠DBA=90°,
∴DB⊥EC.

练习册系列答案
相关题目