Question

【题目】三角形ABC为等腰直角三角形，其中∠A=90°，BC长为6.

　　(1)建立适当的直角坐标系，并写出各个顶点的坐标；

　　(2)将(1)中各顶点的横坐标都加2，纵坐标保持不变，与原图案相比，所得的图案有什么变化？

　　(3)将(1)中各顶点的横坐标不变，将纵坐标都乘-1，与原图案相比，所得的图案有什么变化？

　　(4)将(1)中各顶点的横坐标都乘-2，纵坐标保持不变，与原图案相比，所得的图案有什么变化？

Answer 1

【答案】见解析.

【解析】

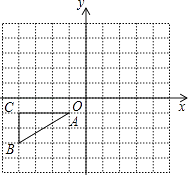
（1）以BC边所在的直线为x轴，BC的中垂线（垂足为O）为y轴，建立直角坐标系．因为BC的长为6，所以A（0，3），B（-3，0），C（3，0）；

（2）横坐标都加2，纵坐标保持不变，与原图案相比，所得的图案向右平移了2个单位长度；

（3）将（1）中各顶点的横坐标不变，将纵坐标都乘-1，与原图案相比，所得的图案与原图案关于x轴对称；

（4）将（1）中各顶点的横坐标都乘-2，纵坐标保持不变，与原图案相比，所得的图案与原图形相比所得的图案在位置上关于y轴对称，横向拉长了2倍．

(1)以BC边所在的直线为x轴，BC的中垂线(垂足为O)为y轴，建立直角坐标系(如图).因为BC的长为6，所以AO=BC=3，所以A(0,3)，B(-3,0)，C(3,0)

（2）整个图案向右平移了2个单位长度，如图△A2B2C2；

（3）与原图案关于x轴对称，如图△A3BC；

（4）与原图形相比所得的图案在位置上关于y轴对称，横向拉长了2倍，如图△AB4C4．