题目内容
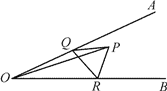
【题目】如图，在△ABC中，P是BC上的点，作PQ∥AC交AB于点Q，分别作PR⊥AB，PS⊥AC，垂足分别是R，S，若PR=PS，则下面三个结论：①AS=AR；②AQ=PQ；③△PQR≌△CPS；④AC﹣AQ=2SC，其中正确的是（ ）
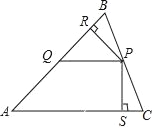
A. ②③④ B. ①② C. ①④ D. ①②③④
【答案】B
【解析】
连接AP,由已知条件利用角平行线的判定可得∠1 = ∠2,由三角形全等的判定得
△APR≌△APS,得AS=AR,由已知可得∠2 = ∠3,得QP=AQ,答案可得.
解:如图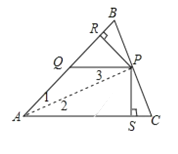
连接AP,
PR=PS,PR⊥AB,垂足为R,PS⊥AC,垂足为S,
AP是∠BAC的平分线,∠1=∠2,
△APR≌△APS.
AS=AR,
又QP/AR,
∠2 = ∠3又∠1 = ∠2，
∠1=∠3,
AQ=PQ,
没有办法证明△PQR≌△CPS,③不成立,
没有办法证明AC-AQ=2SC,④不成立.
所以B选项是正确的.
练习册系列答案
课堂全解字词句段篇章系列答案
步步高口算题卡系列答案
相关题目
