题目内容
如图,在正方形ABCD中,点P是AB的中点,连接DP,过点B作BE⊥DP交DP的延长线于点E,连接AE,过点A作AF⊥AE交DP于点F,连接BF.

(1)若AE=2,求EF的长;
(2)求证:PF=EP+EB.

(1)若AE=2,求EF的长;
(2)求证:PF=EP+EB.
(1)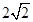 ;(2)证明见试题解析.
;(2)证明见试题解析.
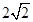 ;(2)证明见试题解析.
;(2)证明见试题解析.试题分析:(1)如图由已知就可以得出∠EAF=∠DAB=90°,AB=AD,可以得出∠1=∠2,由对顶角可以得出∠5=∠6,从而可以证明△AEB≌△AFD,可以求得AE=AF,再利用勾股定理就可以求出EF的值;
(2)如图,过点A作AM⊥EF于M,由(1)可知△AEF是等腰直角三角形,可以得出∠AME=90°,由已知可以证明△BEP≌△AMP,可以得出BE=AM,EP=MP,进而求出结论.
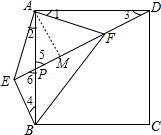
试题解析:(1)∵四边形ABCD是正方形,且BE⊥DP,AF⊥AE,∴AB=AD,BAD=∠EAF=∠BEF=90°,∴∠1+∠FAB=∠2+∠FAB=90°,∴∠1=∠2.∵∠3+∠5=∠4+∠6,且∠5=∠6,∴∠3=∠4.在△AEB和△AFD中,∵
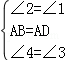 ,∴△AEB≌△AFD,∴AE=AF=2,在Rt△EAF中,由勾股定理,得:EF=
,∴△AEB≌△AFD,∴AE=AF=2,在Rt△EAF中,由勾股定理,得:EF=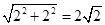 .
.(2)过点A作AM⊥EF于M,且∠EAF=90°,AE=AF,∴△EAF为等腰直角三角形.∴AM=MF=EM,∠AME=∠BEF=90°.∵点P是AB的中点,∴AP=BP.在△AMP和△BEP中,∵
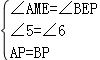 ,∴△AMP≌△BEP,∴BE=AM,EP=MP,∴MF=BE,∴PF=PM+FM=EP+BE.
,∴△AMP≌△BEP,∴BE=AM,EP=MP,∴MF=BE,∴PF=PM+FM=EP+BE.

练习册系列答案
相关题目






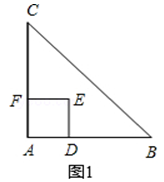

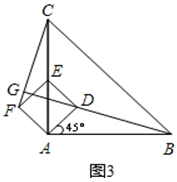
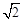 时,求线段FG的长.
时,求线段FG的长.
