题目内容
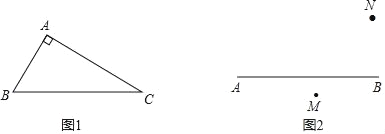
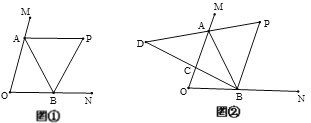
【题目】如图①,∠MON=70°,点A、B在∠MON的两条边上运动,∠MAB与∠NBA的平分线交于点P.
(1)点A、B在运动过程中,∠P的大小会变吗?如果不会,求出∠P的度数;如果会,请说明理由.
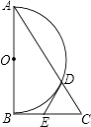
(2)如图②,继续作BC是平分![]() ,AP的反向延长线交BC的延长线于点D,点A、B在运动过程中,∠D的大小会变吗?如果不会,求出∠D的度数;如果会,请说明理由.
,AP的反向延长线交BC的延长线于点D,点A、B在运动过程中,∠D的大小会变吗?如果不会,求出∠D的度数;如果会,请说明理由.
(3)如图②,∠P和∠D有怎样的数量关系?(直接写出答案)
【答案】(1)不会,∠P=55°;(2)不会,∠D=35°;(3)∠P+∠D=90°.
【解析】
(1)先根据∠MON可求出∠OAB+∠OBA的度数,再根据∠MAB与∠NBA的平分线求出∠PAB+∠PBA的度数,即可求出∠P的度数;(2)根据BC是平分![]() ,BP平方∠ABN,可求出∠DBP=90°,故可在直角三角形BDP中求出∠D(3)根据直角三角形BDP即可得出∠P和∠D的关系.
,BP平方∠ABN,可求出∠DBP=90°,故可在直角三角形BDP中求出∠D(3)根据直角三角形BDP即可得出∠P和∠D的关系.
(1)∵∠MON=70°,∴∠OAB+∠OBA=110°,
∴∠MAB+∠NBA=360°-(∠OAB+∠OBA)=250°,
∵∠MAB与∠NBA的平分线交于点P
∴∠PAB+∠PBA=![]() (∠MAB+∠NBA)=125°,
(∠MAB+∠NBA)=125°,
∴∠P=180°-(∠PAB+∠PBA)=55°.
(2)∵BC是平分![]() ,BP平方∠ABN,
,BP平方∠ABN,
∴∠DBP=![]() ∠ABN+
∠ABN+![]() ∠ABO=
∠ABO=![]() (∠ABN+∠ABO)=90°,
(∠ABN+∠ABO)=90°,
∴∠D=90°-∠P=35°,
(3)∵△BDP为直角三角形,故∠P+∠D=90°.

 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案【题目】在《科学》课上,老师讲到温度计的使用方法及液体的沸点时,好奇的王红同学准备测量食用油的沸点,已知食用油的沸点温度高于水的沸点温度(![]() ),王红家只有刻度不超过
),王红家只有刻度不超过![]() 的温度计,她的方法是在锅中倒入一些食用油,用煤气灶均匀加热,并每隔
的温度计,她的方法是在锅中倒入一些食用油,用煤气灶均匀加热,并每隔![]() 测量一次锅中油温,测量得到的数据如下表:
测量一次锅中油温,测量得到的数据如下表:
时间 | 0 | 10 | 20 | 30 | 40 |
油温 | 10 | 30 | 50 | 70 | 90 |
王红发现,烧了![]() 时,油沸腾了,则下列说法不正确的是( )
时,油沸腾了,则下列说法不正确的是( )
A. 没有加热时,油的温度是![]()
B. 加热![]() ,油的温度是
,油的温度是![]()
C. 估计这种食用油的沸点温度约是![]()
D. 每加热![]() ,油的温度升高
,油的温度升高![]()