题目内容
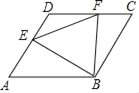
【题目】如图,边长为a的菱形ABCD中,∠DAB=60°,E是异于A、D两点的动点,F是CD上的动点,满足AE+CF=a,△BEF的周长最小值是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】
连接BD,可证△ABE≌△DBF,可得BE=BF,可得△BEF为等边三角形,可得,△BEF的周长为3BE,所以当BE垂直AD时,可求△BEF的周长最小值.
解:连接BD

∵ABCD是菱形,∠DAB=60°
∴AB=AD=CD=BC=a,∠C=∠A=60°,∠ADC=∠ABC=120°
∴△ADB,△BDC为等边三角形,
∴∠ADB=∠ABD=60°=∠BDC=∠DBC,AD=BD=a.
∵AE+CF=a,AE+ED=a,CF+DF=a
∴DF=AE,DE=CF,
∵AE=DF,BD=AB,∠A=∠CDB
∴△AEB≌△DFB
∴BE=BF,∠ABE=∠DBF
∵∠ABE+∠DBE=60°
∴∠DBF+∠DBE=60°即∠EBF=60°
∴△BEF为等边三角形.
∴△BEF的周长=3BE
根据垂线段最短,即当BE⊥AD时,BE值最小.
在Rt△AEB中,AB=a,∠A=60°
∴AE=![]() a,BE=
a,BE=![]() a
a
∴△BEF的周长最小值是![]() ,
,
故选:B.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目