题目内容
【题目】如图,Rt△ABC中,∠ABC=90°,以AB为直径作半圆⊙O交AC与点D,点E为BC的中点,连接DE.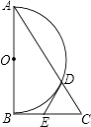
(1)求证:DE是半圆⊙O的切线.
(2)若∠BAC=30°,DE=2,求AD的长.
【答案】
(1)证明:连接OD,OE,BD, 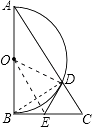
∵AB为圆O的直径,
∴∠ADB=∠BDC=90°,
在Rt△BDC中,E为斜边BC的中点,
∴DE=BE,
在△OBE和△ODE中,
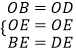 ,
,
∴△OBE≌△ODE(SSS),
∴∠ODE=∠ABC=90°,
∴OD⊥DE
则DE为圆O的切线;
(2)解:在Rt△ABC中,∠BAC=30°,
∴BC= ![]() AC,
AC,
∵BC=2DE=4,
∴AC=8,
又∵∠C=60°,DE=CE,
∴△DEC为等边三角形,即DC=DE=2,
则AD=AC﹣DC=6.
【解析】(1)方法一、要证明DE是半圆⊙O的切线.由已知可知点D在半圆上,因此连接半径OD,再证明OD⊥DE,还需连接OE,BD, 根据直角三角形斜边上的中线等于斜边的一半,证得DE=BE,从而可证明△OBE≌△ODE,得出∠ODE=∠ABC=90°,即可证得结论;方法二、或先证DE=BE,得出∠BDE=∠DBE,再由OB=OD得出∠OBD=∠ODB,而∠ABC=90°=∠OBD+∠DBE,继而可知∠BDE+∠ODB=90°,得出OD⊥DE,即可证得结论。
(2)由已知易求出BC的长,再由直角三角形中,30°角所对的直角边等于斜边的一半,可求出AC的长,再证明△DEC为等边三角形,从而可求得结果。
【考点精析】掌握含30度角的直角三角形和直角三角形斜边上的中线是解答本题的根本,需要知道在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半;直角三角形斜边上的中线等于斜边的一半.

 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案【题目】某同学在用描点法画二次函数y= ![]() +bx+c的图象时,列出了下面的表格:
+bx+c的图象时,列出了下面的表格:
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | … |
y | … | ﹣11 | ﹣2 | 1 | ﹣2 | ﹣5 | … |
由于粗心,他算错了其中一个y值,则这个错误的数值是( ).
A.﹣11 B.﹣2 C.1 D.﹣5
【题目】某公交车每月的支出费用为4000元,票价为2元/人,设每月有![]() 人乘坐该公交车,每月利润为
人乘坐该公交车,每月利润为![]() 元(利润=收入-支出).
元(利润=收入-支出).
(1)请写出![]() 与
与![]() 的关系式 ;
的关系式 ;
(2)完成表格.
| 500 | 1000 | 1500 | 2000 | 2500 | 3000 | … |
|
|
|
|
|
|
| … |
(3)观察表中数据,每月乘客量达到 人以上时,该公交车才不会亏损.