题目内容
【题目】已知抛物线![]() :
:![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,其对称轴
,其对称轴![]() 与
与![]() 轴交于点
轴交于点![]() .
.

(1)求抛物线![]() 的表达式;
的表达式;
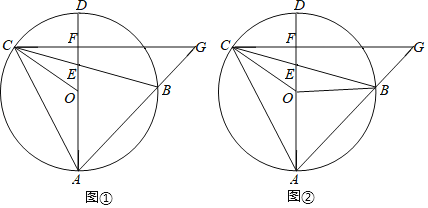
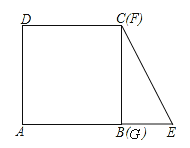
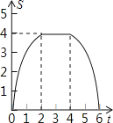
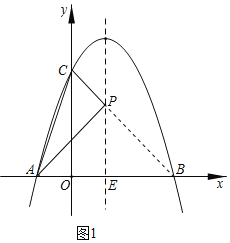
(2)如图1,若动点![]() 在对称轴
在对称轴![]() 上,当
上,当![]() 的周长最小时,求点
的周长最小时,求点![]() 的坐标;
的坐标;
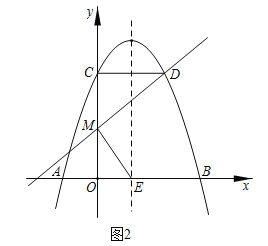
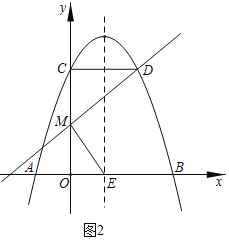
(3)如图2,设点![]() 关于对称轴
关于对称轴![]() 的对称点为
的对称点为![]() ,
,![]() 是线段
是线段![]() 上的一个动点,若
上的一个动点,若![]() ,求直线
,求直线![]() 的表达式.
的表达式.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 或
或![]()
【解析】
(1)根据点A,B,C的坐标,利用待定系数法即可求出抛物线m的函数表达式;
(2)连接BC交抛物线对称轴n于点P,利用两点之间线段最短可得出此时△PAC的周长最小,由点B,C的坐标可求出直线BC的函数表达式,由抛物线的函数表达式可得出抛物线对称轴为直线x=2,再利用一次函数图象上点的坐标特征可求出点P的坐标;
(3)由抛物线的对称轴及点C的坐标可得出点D的坐标,进而可得出OE,CD的长,设点M的坐标为(0,y)(0≤y≤6),则OM=y,CM=6-y,由△DMC∽△MEO,利用相似三角形的性质可求出OM的长,进而可得出点M的坐标,再根据点D,M的坐标,利用待定系数法即可求出直线DM的函数表达式.
(1)![]() 抛物线
抛物线![]() :
:![]() 经过
经过![]() ,
,![]() ,
,![]() 三点,
三点,
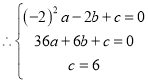 ,解得:
,解得: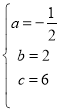
![]() 抛物线
抛物线![]() 的表达式为:
的表达式为:![]() .
.
(2)如图1.连接![]() 与对称轴
与对称轴![]() 交于点
交于点![]() ,
,
![]() 和
和![]() 关于对称轴
关于对称轴![]() 对称,
对称,
![]() 对称轴
对称轴![]() 为
为![]() ,且有
,且有![]() ,
,
![]() ,
,
![]() 两点之间线段最短,
两点之间线段最短,
![]() 的周长最小值为
的周长最小值为![]() ,
,
此时![]() 与对称铀
与对称铀![]() 的交点
的交点![]() 为所求,
为所求,
:经过![]() ,
,![]() 的直线为
的直线为![]() ,
,
![]() 当
当![]() 时,
时,![]() ,则
,则![]() .
.
(3)如图2,对称轴![]() 为
为![]() .
.
![]() 点
点![]() 关于对称轴
关于对称轴![]() 的对称点为
的对称点为![]()
![]() 点
点![]() 在线段
在线段![]() 上,设点
上,设点![]() 的坐标为
的坐标为![]() ,
,
则![]() ,
,![]() ,
,![]() ,
,
又![]() ,
,![]() ,
,
![]() 由
由![]() ,得:
,得:![]() ,即
,即![]() ,
,
解得:![]() 或4,则点
或4,则点![]() 的坐标为
的坐标为![]() 或
或![]() ,
,
设直线![]() 的表达式为
的表达式为![]() ,
,
①当![]() ,
,![]() 时,有
时,有![]() ,即
,即![]() .
.
![]() 直线
直线![]() 的表达式为
的表达式为![]() ;
;
②当![]() ,
,![]() 时,有
时,有![]() ,即
,即![]() .
.
![]() 直线
直线![]() 的表达式为
的表达式为![]() :
:
综上所述:所求自线![]() 的表达式为
的表达式为![]() 或
或![]() .
.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目