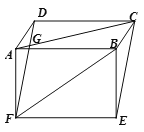
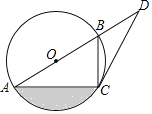
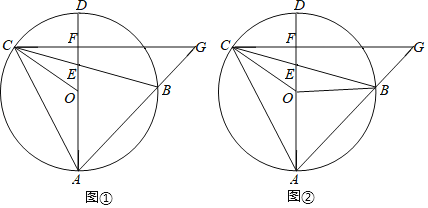
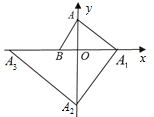
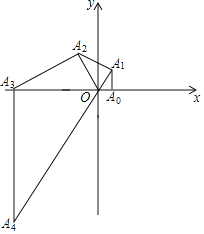
ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩ»γΆΦΘ§“―÷Σ÷±œΏ![]() ΫΜx÷αΓΔy÷αΖ÷±π”ΎΒψAΓΔΒψFΘ§≤Δ”κΖ¥±»άΐΚ· ΐ
ΫΜx÷αΓΔy÷αΖ÷±π”ΎΒψAΓΔΒψFΘ§≤Δ”κΖ¥±»άΐΚ· ΐ![]() ΒΡΆΦœώΫΜ”ΎBΓΔCΝΫΒψΘ®ΒψB‘ΎΒψCΒΡΉσ≤ύΘ©Θ§“‘OAΈΣ÷±ΨΕΉςΑκ‘≤Θ§‘≤–ΡΈΣPΘ§ΙΐΒψBΉςx÷αΒΡ¥ΙœΏΘ§¥ΙΉψΈΣEΘ§≤Δ”κΑκ‘≤PΫΜ”ΎΒψDΘ°
ΒΡΆΦœώΫΜ”ΎBΓΔCΝΫΒψΘ®ΒψB‘ΎΒψCΒΡΉσ≤ύΘ©Θ§“‘OAΈΣ÷±ΨΕΉςΑκ‘≤Θ§‘≤–ΡΈΣPΘ§ΙΐΒψBΉςx÷αΒΡ¥ΙœΏΘ§¥ΙΉψΈΣEΘ§≤Δ”κΑκ‘≤PΫΜ”ΎΒψDΘ°
Θ®1Θ©»τBΓΔCΒΡΚαΉχ±ξΖ÷±πΈΣx1ΓΔx2Θ§«“x2x15Θ§«σmΒΡ÷ΒΘΜ
Θ®2Θ©≈–ΕœœΏΕΈDEΒΡ≥Λ «ΖώΥφmΒΡΗΡ±δΕχΗΡ±δΘ§»τ≤ΜΥφmΒΡΗΡ±δΕχΗΡ±δΘ§«κ«σ≥ωDEΒΡ≥ΛΘΜ»τΥφmΒΡΗΡ±δΕχΗΡ±δΘ§«κΥΒΟςάμ”…ΘΜ
Θ®3Θ©Φ«ΒψCΙΊ”Ύ÷±œΏDEΒΡΕ‘≥ΤΒψΈΣCΓδΘ§Β±ΥΡ±Ώ–ΈCDCΓδEΈΣΝβ–Έ ±Θ§÷±Ϋ”–¥≥ωCΒΡΉχ±ξΚΆmΒΡ÷ΒΘ°

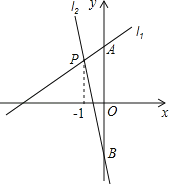
ΓΨ¥πΑΗΓΩΘ®1Θ©![]() ΘΜΘ®2Θ©≤ΜΗΡ±δΘ§
ΘΜΘ®2Θ©≤ΜΗΡ±δΘ§![]() ΘΜΘ®3Θ©
ΘΜΘ®3Θ©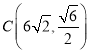 Θ§
Θ§![]()
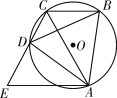
ΓΨΫβΈωΓΩ
Θ®1Θ©…η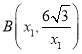 Θ§
Θ§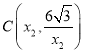 Θ§ΗυΨίΒψBΘ§ΒψC‘Ύ“Μ¥ΈΚ· ΐ”κΖ¥±»άΐΚ· ΐΒΡΆΦœσ…œΘ§Ν–≥ωΖΫ≥ΧΉιΘ§«σΫβΦ¥Ω…ΘΜ
Θ§ΗυΨίΒψBΘ§ΒψC‘Ύ“Μ¥ΈΚ· ΐ”κΖ¥±»άΐΚ· ΐΒΡΆΦœσ…œΘ§Ν–≥ωΖΫ≥ΧΉιΘ§«σΫβΦ¥Ω…ΘΜ
Θ®2Θ©Ν§Ϋ”![]() ΓΔ
ΓΔ![]() Θ§ΗυΨί
Θ§ΗυΨί![]() ΒΟ≥ω
ΒΟ≥ω![]() Θ§…η
Θ§…η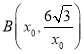 Θ§
Θ§![]() Θ§Ά®ΙΐΦΤΥψΒΟ≥ω
Θ§Ά®ΙΐΦΤΥψΒΟ≥ω![]() Θ§
Θ§![]() Θ§¥ζ»κ«σΫβΦ¥Ω…ΘΜ
Θ§¥ζ»κ«σΫβΦ¥Ω…ΘΜ
Θ®3Θ©Ν§Ϋ”CCΓδΘ§…ηDE”κCCΓδΫΜ”ΎGΘ§”…Θ®2Θ©”κΝβ–ΈΒΡ–‘÷ ΒΟ≥ωDGΘΫEGΘΫ![]() Θ§ΫχΕχΒΟ≥ωΒψCΒΡΉίΉχ±ξΘ§«σΫβΦ¥Ω…Θ°
Θ§ΫχΕχΒΟ≥ωΒψCΒΡΉίΉχ±ξΘ§«σΫβΦ¥Ω…Θ°
ΫβΘΚΘ®1Θ©”…Χβ“βΒΟΘ§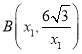 Θ§
Θ§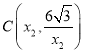
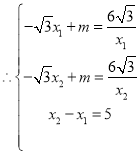 Θ§
Θ§
œϊ»Ξ![]() ΒΟΘ§
ΒΟΘ§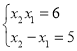 Θ§
Θ§
ΫβΒΟΘ§![]() Θ®…α»ΞΘ©Μρ1Θ§
Θ®…α»ΞΘ©Μρ1Θ§![]() Θ§
Θ§
ΓύΒΟ![]() Θ§¥ζ»κ
Θ§¥ζ»κ![]() ΒΟΘ§
ΒΟΘ§![]() ΘΜ
ΘΜ
Θ®2Θ©Ν§Ϋ”![]() ΓΔ
ΓΔ![]() Θ§“Ή÷Λ
Θ§“Ή÷Λ![]() Θ§
Θ§
Γύ![]() Φ¥
Φ¥![]() Θ§
Θ§
…η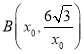 Θ§‘ρ
Θ§‘ρ Θ§Φ¥
Θ§Φ¥![]() Θ§
Θ§
![]() Θ§
Θ§![]() Θ§
Θ§
![]() Θ§
Θ§
![]() Θ§
Θ§
![]() Θ§
Θ§
ΓύDEΒΡ≥Λ≤ΜΗΡ±δΘ§ΈΣ![]() ΘΜ
ΘΜ
Θ®3Θ©Ν§Ϋ”CCΓδΘ§…ηDE”κCCΓδΫΜ”ΎGΘ§
”…Θ®2Θ©ΒΟΘ§![]() Θ§
Θ§
ΓΏΥΡ±Ώ–ΈCDCΓδEΈΣΝβ–ΈΘ§
ΓύDGΘΫEGΘΫ![]() Θ§
Θ§
ΓύCΒΡΉίΉχ±ξΈΣ![]() Θ§
Θ§
Β±yΘΫ![]() ±Θ§
±Θ§![]() Θ§
Θ§
Γύ![]() Θ§
Θ§
Γύ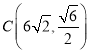 Θ§
Θ§
ΫΪΒψ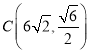 ¥ζ»κ
¥ζ»κ![]() ÷–ΒΟΘΚ
÷–ΒΟΘΚ![]() Θ§
Θ§
Γύ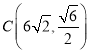 Θ§
Θ§![]() Θ°
Θ°