题目内容
【题目】如图,直线AB、CD相交于O点,∠AOC=70,OF平分∠AOD,射线OE在∠BOD的内部(如图),∠BOE=n°.
(1)当n=30时,求∠DOE的度数;
(2)当n=35时,射线OE与OF之间有什么位置关系?
(3)若射线OD平分∠EOF,求n的值.
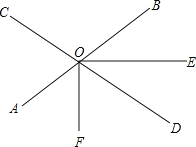
【答案】(1)40°;(2)射线OE有OF之间垂直.(3)15
【解析】
(1)根据对顶角相等得到∠DOB=∠AOC=70°,利用∠DOE=∠DOB-∠BOE计算出即可;
(2)根据邻补角的定义得到AOD=180°-∠AOC=180°-70°=110°,再利用角平分线的定义得到![]() 易得∠FOE=∠DOF+∠DOE=55°+35°=90°,根据垂直的定义即可得到射线OE与OF垂直.
易得∠FOE=∠DOF+∠DOE=55°+35°=90°,根据垂直的定义即可得到射线OE与OF垂直.
(3)
(1)∵![]()
∴![]()
(2)射线OE与OF垂直.理由如下:
∵![]()
∴![]()
∵![]()
而OF平分∠AOD,
∴![]()
∴![]()
∴射线OE与OF垂直.
(3) ∵![]()
∴![]()
∵![]()
而OF平分∠AOD,
∴![]()
射线OD平分∠EOF,
![]()
∴![]()
解得:![]()

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目