Question

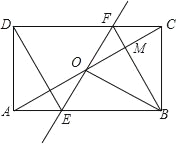
【题目】如图，矩形ABCD中，O为AC中点，过O点的直线分别于AB、CD交于E、F，连结BF交AC与点M，连结DE、BO，若∠COB=60°，FO=FC

求证：①FB⊥OC，OM=CM；

②四边形EBFD是菱形；

③MB：OE=3：2．

Answer 1

【答案】详见解析

【解析】

①根据已知得出△OBF≌△CBF，可求得△OBF与△CBF关于直线BF对称，进而求得FB⊥OC，OM=CM；

②先证得∠ABO=∠OBF=30°，再证得OE=OF，进而证得OB⊥EF，因为BD、EF互相平分，即可证得四边形EBFD是菱形．

③根据三角函数求得MB=，OF=，根据OE=OF即可求得MB：OE=3：2．

证明：①连接BD，

∵四边形ABCD是矩形，

∴AC=BD，AC、BD互相平分，

∵O为AC中点，

∴BD也过O点，

∴OB=OC，

∵∠COB=60°，OB=OC，

∴△OBC是等边三角形，

∴OB=BC=OC，∠OBC=60°，

在△OBF与△CBF中

,

∴△OBF≌△CBF（SSS），

∴△OBF与△CBF关于直线BF对称，

∴FB⊥OC，OM=CM；

②∵∠OBC=60°，

∴∠ABO=30°，

∵△OBF≌△CBF，

∴∠OBM=∠CBM=30°，

∴∠ABO=∠OBF，

∵AB∥CD，

∴∠OCF=∠OAE，

∵OA=OC，

易证△AOE≌△COF，

∴OE=OF，

∴OB⊥EF，

∴四边形EBFD是菱形，

③∵∠OMB=∠BOF=90°，∠OBF=30°，

∴MB=，OF=，

∵OE=OF，

∴MB：OE=3：2，