��Ŀ����
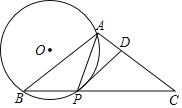
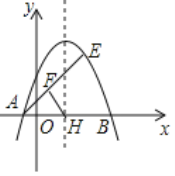
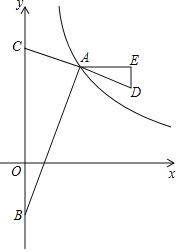
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У���A�Ƿ���������y=![]() ��x��0��m��1��ͼ����һ�㣬��A�ĺ�����Ϊm����B��0����m����y�Ḻ�����ϵ�һ�㣬����AB��AC��AB����y���ڵ�C���ӳ�CA����D��ʹ��AD=AC������A��AEƽ����x�ᣬ����D��y��ƽ���߽�AE�ڵ�E��
��x��0��m��1��ͼ����һ�㣬��A�ĺ�����Ϊm����B��0����m����y�Ḻ�����ϵ�һ�㣬����AB��AC��AB����y���ڵ�C���ӳ�CA����D��ʹ��AD=AC������A��AEƽ����x�ᣬ����D��y��ƽ���߽�AE�ڵ�E��
��1����m=3ʱ�����A�����ꣻ
��2��DE=�� �������D������Ϊ��x��y������y����x�ĺ�����ϵʽ���Ա�����ȡֵ��Χ��
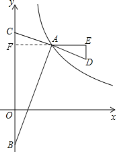
��3������BD������A��BD��ƽ���ߣ��루2���еĺ���ͼ���ڵ�F����mΪ��ֵʱ����A��B��D��FΪ������ı�����ƽ���ı��Σ�
���𰸡���1����A����Ϊ��3��6������2��1��y=![]() ��x��2������3��m=2ʱ����A��B��D��FΪ������ı�����ƽ���ı��Σ�
��x��2������3��m=2ʱ����A��B��D��FΪ������ı�����ƽ���ı��Σ�
����������1�������������mֵ���������
��2������ED��y�ᣬAD=AC����ȫ�������ν���DEת��Ϊ��FC���������������������FC����m��ʾD�����꣬���ô�����Ԫ���õ�y��x������ϵ��
��3����ֵ���߶��е�������ڶ˵������ƽ����������ϵ��ͬ���ɵ��߶��е��������ֱ��Ƕ˵���������ƽ���������ô˷�����ʾ��F��������루2���к�����ϵʽ���ɣ�
��1����m=3ʱ��y=![]() ��
��
�൱x=3ʱ��y=6��
���A������3��6����
��2����ͼ���ӳ�EA��y���ڵ�F��
��DE��x��
���FCA=��EDA����CFA=��DEA��
��AD=AC��
���FCA�ա�EDA��
��DE=CF��
��A��m��m2��m����B��0����m����
��BF=m2��m������m��=m2��AF=m��
��Rt��CAB��AF��x����
���AFC�ס�BFA��
��AF2=CFBF��
��m2=CFm2��
��CF=1��
��DE=1��
�ʴ�Ϊ��1��
�����沽���֪����E����Ϊ��2m��m2��m����
���D������2m��m2��m��1����
��x=2m��
y=m2��m��1��
���m=![]() ����y=m2��m��1��
����y=m2��m��1��
��y=![]() ��x��2����
��x��2����
��3���������֪��AF��BD
��AD��BFΪƽ���ı��ζԽ���ʱ��
��ƽ���ı��ζԽ�����ƽ�ֿɵ�A��D��B��F�ĺ����ꡢ������֮�ͷֱ����
���F������a��b��
��a+0=m+2m
b+����m��=m2��m+m2��m��1
��a=3m��b=2m2��m��1
����y=![]() ����
����
2m2��m��1=![]() ��
��
���m1=2��m2=0����ȥ��
��FD��ABΪƽ���ı��ζԽ���ʱ��
ͬ�����F����Ϊ��a��b����
��a=��m��b=1��m����F����y����࣬�ɣ�2����֪����D����ͼ������y�����
��������������
���ϵ�m=2ʱ����A��B��D��FΪ������ı�����ƽ���ı��Σ�