ћвƒњƒЏ»Ё
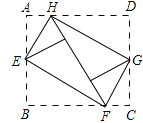
°Њћвƒњ°њЌЉҐў «“ї√ґ÷ µЎЊщ‘»µƒ’эЋƒ√жће–ќ„іµƒчї„”£ђ√њЄц√ж…ѕЈ÷±р±к”– э„÷1£ђ2£ђ3£ђ4£ђЌЉҐЏ «“їЄц’эЅщ±я–ќ∆е≈ћ£ђѕ÷Ќ®єэ÷јчї„”µƒЈљ љЌжћш∆е”ќѕЈ£ђєж‘т «£ЇљЂ’в√ґчї„”÷ј≥цЇу£ђњічї„”ѕт…ѕ»эЄц√ж£®≥эµ„√жЌв£©µƒ э„÷÷ЃЇЌ «ЉЄ£ђЊЌі”ЌЉҐЏ÷–µƒAµгњ™ Љ—Ў„≈Ћ≥ ±’лЈљѕтЅђ–шћшґѓЉЄЄцґ•µг£ђµЏґюіќі”µЏ“їіќµƒ÷’µгі¶њ™ Љ£ђ∞іµЏ“їіќµƒЈљЈ®ћшґѓ£Ѓ
£®1£©Ћжїъ÷ј“їіќчї„”£ђ‘т∆е„”ћшґѓµљµгCі¶µƒЄ≈¬ «°° °°
£®2£©Ћжїъ÷јЅљіќчї„”£ђ”√ї≠ ч„іЌЉїтЅ–±нµƒЈљЈ®£ђ«у∆е„”„о÷’ћшґѓµљµгCі¶µƒЄ≈¬ £Ѓ
°Њір∞Є°њ£®1£©![]() £ї£®2£©∆е„”„о÷’ћшґѓµљµгCі¶µƒЄ≈¬ ќ™
£ї£®2£©∆е„”„о÷’ћшґѓµљµгCі¶µƒЄ≈¬ ќ™![]() £Ѓ
£Ѓ
°Њљвќц°њ£®1£©ЇЌќ™8 ±£ђњ…“‘µљіпµгC£ђЄщЊЁЄ≈¬ єЂ љЉ∆ЋгЉіњ…£ї
£®2£©Ѕ–±нµ√µљЋщ”–µƒ«йњц э£ђ»їЇу‘ў’“µљЈыЇѕћхЉюµƒ«йњц э£ђјы”√Є≈¬ єЂ љљш––«уљвЉіњ….
Ћжїъ÷ј“їіќчї„”£ђчї„”ѕт…ѕ»эЄц√ж£®≥эµ„√жЌв£©µƒ э„÷÷ЃЇЌњ…“‘ « 6°Ґ7°Ґ8°Ґ9.
£®1£©Ћжїъ÷ј“їіќчї„”£ђ¬ъ„г∆е„”ћшґѓµљµг C і¶µƒ э„÷ « 8£ђ‘т∆е„”ћшґѓµљµгCі¶µƒЄ≈¬ «![]() £ђ
£ђ
є ір∞Єќ™£Ї![]() £ї
£ї
£®2£©Ѕ–±нµ√£Ї
9 | 8 | 7 | 6 | |
9 | 9£ђ9 | 8£ђ9 | 7£ђ9 | 6£ђ9 |
8 | 9£ђ8 | 8£ђ8 | 7£ђ8 | 6£ђ8 |
7 | 9£ђ7 | 8£ђ7 | 7£ђ7 | 6£ђ7 |
6 | 9£ђ6 | 8£ђ6 | 7£ђ6 | 6£ђ6 |
є≤”–16÷÷њ…ƒ№£ђЇЌќ™14њ…“‘µљіпµгC£ђ”–3÷÷«й–ќ£ђ
Ћщ“‘∆е„”„о÷’ћшґѓµљµгCі¶µƒЄ≈¬ ќ™![]() £Ѓ
£Ѓ

°Њћвƒњ°њќ ћв±≥Њ∞£Ї
–°ЇмЌђ—І‘Џ—Іѕ∞єэ≥ћ÷–”цµљ’в—щ“їµјЉ∆Ћгћв°∞Љ∆Ћг![]() °±£ђЋыЊхµ√ћЂ¬йЈ≥£ђєјЉ∆”¶Є√”–њ…“‘ЉтїѓЉ∆ЋгµƒЈљЈ®£ђЊЌ»•«лљћіёјѕ ¶£Ѓіёјѕ ¶Ћµ£ЇƒгЌк≥…ѕ¬√жµƒќ ћвЇуЊЌњ…ƒ№÷™µјЄ√»зЇќЉтїѓЉ∆Ћгј≤£°
°±£ђЋыЊхµ√ћЂ¬йЈ≥£ђєјЉ∆”¶Є√”–њ…“‘ЉтїѓЉ∆ЋгµƒЈљЈ®£ђЊЌ»•«лљћіёјѕ ¶£Ѓіёјѕ ¶Ћµ£ЇƒгЌк≥…ѕ¬√жµƒќ ћвЇуЊЌњ…ƒ№÷™µјЄ√»зЇќЉтїѓЉ∆Ћгј≤£°
їс»°–¬÷™£Ї
«лƒгЇЌ–°Їм“ї∆рЌк≥…іёјѕ ¶ћбє©µƒќ ћв£Ї
£®1£©ћо–іѕ¬±н£Ї
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
£®2£©єџ≤м±нЄс£ђƒгЈҐѕ÷![]() ”л
”л![]() ”– ≤√і эЅњєЎѕµ£њ«л÷±љ”–і≥ц
”– ≤√і эЅњєЎѕµ£њ«л÷±љ”–і≥ц![]() ”л
”л![]() ÷ЃЉдµƒ эЅњєЎѕµ£Ѓ
÷ЃЉдµƒ эЅњєЎѕµ£Ѓ
љвЊцќ ћв£Ї
£®3£©«лљбЇѕ…ѕ цµƒ”–єЎ–≈ѕҐ£ђЉ∆Ћг![]() £Ѓ
£Ѓ