题目内容
【题目】已知:如图,在△ABC中,AB=AC,点P是底边BC上一点且满足PA=PB,⊙O是△PAB的外接圆,过点P作PD∥AB交AC于点D.
(1)求证:PD是⊙O的切线;
(2)若BC=8,tan∠ABC=![]() ,求⊙O的半径.
,求⊙O的半径.
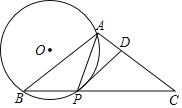
【答案】(1)证明见解析;(2)⊙O的半径是![]() .
.
【解析】(1)先根据圆的性质得:![]() ,由垂径定理可得:OP⊥AB,根据平行线可得:OP⊥PD,所以PD是⊙O的切线;
,由垂径定理可得:OP⊥AB,根据平行线可得:OP⊥PD,所以PD是⊙O的切线;
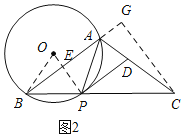
(2)如图2,作辅助线,构建直角三角形,根据三角函数设CG=![]() x,BG=2x,利用勾股定理计算x=
x,BG=2x,利用勾股定理计算x=![]() ,设AC=a,则AB=a,AG=
,设AC=a,则AB=a,AG=![]() ﹣a,在Rt△ACG中,由勾股定理列方程可得a的值,同理设⊙O的半径为r,同理列方程可得r的值.
﹣a,在Rt△ACG中,由勾股定理列方程可得a的值,同理设⊙O的半径为r,同理列方程可得r的值.
(1)如图1,连接OP,
∵PA=PB,
∴![]() ,
,
∴OP⊥AB,
∵PD∥AB,
∴OP⊥PD,
∴PD是⊙O的切线;
(2)如图2,过C作CG⊥BA,交BA的延长线于G,
Rt△BCG中,tan∠ABC=![]() ,
,
设CG=![]() x,BG=2x,
x,BG=2x,
∴BC=![]() x,
x,
∵BC=8,即![]() x=8,
x=8,
x=![]() ,
,
AC=a,则AB=a,AG=![]() ﹣a,
﹣a,
在Rt△ACG中,由勾股定理得:AG2+CG2=AC2,
∴ (![]() ﹣a)2+(
﹣a)2+(![]() )2=a2,
)2=a2,
a=2![]() ,
,
∴AB=2![]() ,BE=
,BE=![]() ,
,
Rt△BEP中,同理可得:PE=![]() ,
,
设⊙O的半径为r,则OB=r,OE=r﹣![]() ,
,
由勾股定理得:r2=(r-![]() )2+(
)2+(![]() )2,
)2,
r=![]() ,
,
答:⊙O的半径是![]() .
.


练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案
相关题目