Question

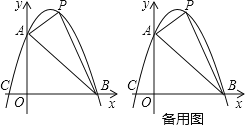
【题目】如图，已知抛物线y=x2-2x-3与x轴交于A、B两点．

（1）当0＜x＜3时，求y的取值范围；

（2）点P为抛物线上一点，若S△PAB=10，求出此时点P的坐标．

Answer 1

【答案】(1) ﹣4≤y＜0;(2) P点坐标为（﹣2，5）或（4，5）

【解析】(1)、首先将抛物线配成顶点式，然后根据x的取值范围，从而得出y的取值范围；(2)、根据题意得出AB的长度，然后根据面积求出点P的纵坐标，根据抛物线的解析式求出点P的坐标．

（1）∵抛物线的解析式为y=x2﹣2x﹣3，∴y=x2﹣2x﹣3=（x﹣1）2﹣4，

∴顶点坐标为（1，﹣4），由图可得当0＜x＜3时，﹣4≤y＜0．

（2）当y=0时，x2﹣2x﹣3=0， 解得：x1=-1 x2=3

∵A（﹣1，0）、B（3，0）， ∴AB=4．

设P（x，y），则S△PAB=AB|y|=2|y|=10， ∴|y|=5， ∴y=±5．

①当y=5时，x2﹣2x﹣3=5，解得：x1=﹣2，x2=4，

此时P点坐标为（﹣2，5）或（4，5）；

②当y=﹣5时，x2﹣2x﹣3=﹣5，方程无解；

综上所述，P点坐标为（﹣2，5）或（4，5）．