题目内容
【题目】M(﹣1,![]() ),N(1,
),N(1,![]() )是平面直角坐标系xOy中的两点,若平面内直线MN上方的点P满足:45°≤∠MPN≤90°,则称点P为线段MN的可视点.
)是平面直角坐标系xOy中的两点,若平面内直线MN上方的点P满足:45°≤∠MPN≤90°,则称点P为线段MN的可视点.
(1)在点![]() ,
,![]() ,
,![]() ,A4(2,2)中,线段MN的可视点为 ;
,A4(2,2)中,线段MN的可视点为 ;
(2)若点B是直线y=x![]() 上线段MN的可视点,求点B的横坐标t的取值范围;
上线段MN的可视点,求点B的横坐标t的取值范围;
(3)直线y=x+b(b≠0)与x轴交于点C,与y轴交于点D,若线段CD上存在线段MN的可视点,直接写出b的取值范围.
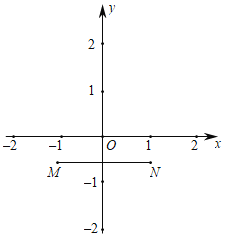
【答案】(1)A1,A3;(2)点B的横坐标t的取值范围是0≤t≤1;(3)![]() 或
或![]() .
.
【解析】
(1)根据“直径所对的圆周角是直角”可知线段MN的可视点在以MN为直径的圆的外部或圆上,根据“同弧所对的圆周角等于圆心角的一半”可知线段MN的可视点在以E为圆心,EM长为半径的⊙E的内部或⊙E上,根据坐标可以判断哪些点符合要求.
(2)点B既要在直线y=x+![]() 上,又要⊙E的内部或圆上,且在⊙G的外部或圆上,故应该在直线y=x+
上,又要⊙E的内部或圆上,且在⊙G的外部或圆上,故应该在直线y=x+![]() 与⊙G、⊙E的交点E、F为端点的线段上,求出E、F的横坐标即可.
与⊙G、⊙E的交点E、F为端点的线段上,求出E、F的横坐标即可.
(3)分b<0,b>0两种情况进行讨论.
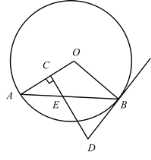
解:(1)如图1,以MN为直径的半圆交y轴于点E,以E为圆心,EM长为半径的⊙E交y轴于点F,
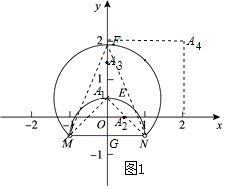
∵MN是⊙G的直径,
∴∠MA1N=90°,
∵M(﹣1,![]() ),N(1,
),N(1,![]() )
)
∴MN⊥EG,EG=1,MN=2
∴EM=EF![]() ,
,
∴∠MFN![]() ∠MEN=45°,
∠MEN=45°,
∵45°≤∠MPN≤90°,
∴点P应落在⊙E内部,且落在⊙G外部
∴线段MN的可视点为A1,A3;
故答案为A1,A3;
(2)如图,以(0,![]() )为圆心,1为半径作圆,以(0,
)为圆心,1为半径作圆,以(0,![]() )为圆心,
)为圆心,![]() 为半径作圆,两圆在直线MN上方的部分与直线
为半径作圆,两圆在直线MN上方的部分与直线![]() 分别交于点E,F.
分别交于点E,F.
过点F作FH⊥x轴,过点E作EH⊥FH于点H,
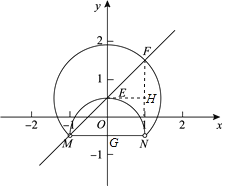
∵FH⊥x轴,
∴FH∥y轴,
∴∠EFH=∠MEG=45°,
∵∠EHF=90°,EF![]() ,
,
∴EH=FH=1,
∴E(0,![]() ),F(1,
),F(1,![]() ).
).
只有当点B在线段EF上时,满足45°≤∠MBN≤90°,点B是线段MN的可视点.
∴点B的横坐标t的取值范围是0≤t≤1.
(3)如图,⊙G与x轴交于H,与y轴交于E,连接GH,OG![]() ,GH=1,
,GH=1,
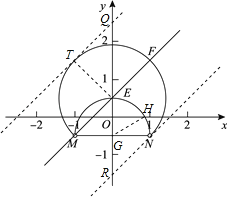
∴OH![]() ,
,
∴H(![]() ,0).E(0,
,0).E(0,![]() )
)
当直线y=x+b(b≠0)与x轴交于点C,与y轴交于点D,若线段CD上存在线段MN的可视点,
①直线y=x+b与y轴交点在y负半轴上
将H(![]() ,0)代入y=x+b得
,0)代入y=x+b得![]() b=0,解得b1
b=0,解得b1![]() ,
,
将N(1,![]() )代入y=x+b得1+b
)代入y=x+b得1+b![]() ,解得b2
,解得b2![]()
∴![]() b
b![]()
②直线y=x+b与y轴交点在y正半轴上
将 E(0,![]() )代入得b
)代入得b![]() ,
,
当直线y=x+b与⊙E相切于T时交y轴于Q,连接ET,则ET⊥TQ,
∵∠EQT=45°,
∴TQ=ET=EM![]() ,
,
∴EQ![]() 2
2
∴OQ=OE+EQ![]() 2
2![]()
∴![]()
综上所述:![]() 或
或![]() .
.

 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案