题目内容
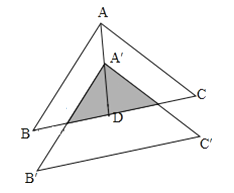
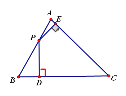
【题目】如图,在△ABC中,∠C=45°,∠B=60°,BC为![]() +1,点P为边AB上一动点,过点P作PD⊥BC于点D,PE⊥AC于点E,则DE的最小值为_____.
+1,点P为边AB上一动点,过点P作PD⊥BC于点D,PE⊥AC于点E,则DE的最小值为_____.
【答案】![]()
【解析】
当CP⊥AB时,线段DE的值最小,利用四点共圆的判定可得:C、D、P、E四点共圆,且直径为CP,由∠B=60°,BC为![]() +1,求出PC,从而得出半径OD的长度,然后由∠ACB=45°,得到∠EOD=90°,利用等腰直角三角形的性质,可求出DE的值.
+1,求出PC,从而得出半径OD的长度,然后由∠ACB=45°,得到∠EOD=90°,利用等腰直角三角形的性质,可求出DE的值.
解:当CP⊥AB时,线段DE的值最小(因为四边形C、D、P、E四点共圆,PC是直径,BC=![]() 和∠B=60°是定值,所以直径CP最小时,∠DCE所对的弦DE最小);如图:
和∠B=60°是定值,所以直径CP最小时,∠DCE所对的弦DE最小);如图:

∵PD⊥BC于D,PE⊥AC于E,
∴∠CDP=∠AEP=90°,
∴∠CDP+∠AEP=180°,
∴C、D、P、E四点共圆,且直径为CP,
∵∠B=60°,CP⊥AB,BC=![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵∠ACB=45°,
∴∠EOD=90°,
∴△OED是等腰直角三角形,
∴![]() ;
;
∴DE的最小值为:![]() .
.
故答案为:![]() .
.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目