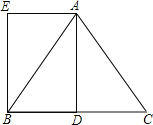题目内容
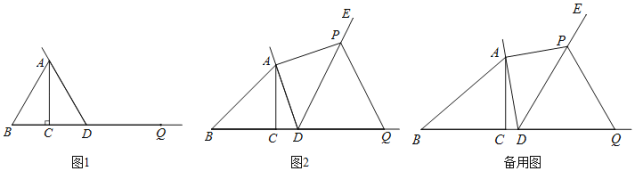
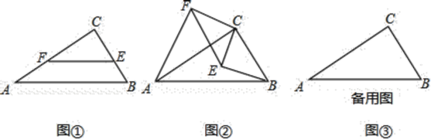
【题目】![]() 尝试探究:如图
尝试探究:如图![]() ,在
,在![]() 中,
中,![]() ,
,![]() ,E,F分别是BC,AC上的点,且
,E,F分别是BC,AC上的点,且![]() ,则
,则![]() ______;
______;
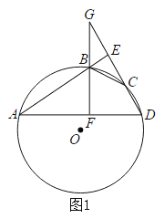
![]() 类比延伸:如图
类比延伸:如图![]() ,若将图
,若将图![]() 中的
中的![]() 绕点C顺时针旋转,则在旋转的过程中,
绕点C顺时针旋转,则在旋转的过程中,![]() 值是否发生变化?请仅就图
值是否发生变化?请仅就图![]() 的情形写出推理过程;
的情形写出推理过程;
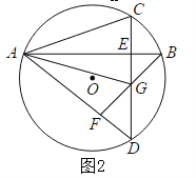
![]() 拓展运用:若
拓展运用:若![]() ,
,![]() ,在旋转过程中,当B,E,F三点在同一直线上时,请直接写出此时线段AF的长.
,在旋转过程中,当B,E,F三点在同一直线上时,请直接写出此时线段AF的长.
【答案】(1)![]() ;(2)不变化,理由见解析;(3)AF的长为3
;(2)不变化,理由见解析;(3)AF的长为3![]() -
-![]() 或3
或3![]() +
+![]() .
.
【解析】
(1)根据直角三角形30°角的性质即可解决问题;
(2)只要证明△ACF∽△BCE,可得![]() ,由此即可解决问题;
,由此即可解决问题;
(3)分两种情形画出图形分别解决问题即可;
(1)如图①中,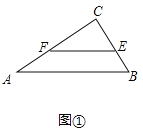
∵在△ABC中,∠ABC=90°,∠A=30°,EF∥AB,
∴∠CFE=∠A=30°,
∴CF=![]() EC,AC=
EC,AC=![]() BC,
BC,
∴AF=AC-CF=![]() BC-
BC-![]() EC=
EC=![]() (BC-EC)=
(BC-EC)=![]() BE,
BE,
∴![]() =
=![]() ,
,
故答案为![]() .
.
(2)不变化,
理由如下:如图②中,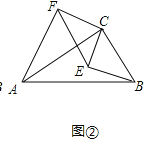
由(1)及旋转的性质知,∠CFE=∠CAB=30°.
∠FCE=∠ACB=90°.
在Rt△CEF中,tan∠CEF=![]() =
=![]() ,
,
在Rt△CBA中,tan∠ABC=![]() =
=![]() ,
,
∴![]() ,
,
又∵∠FCE=∠ACB=90°,∠FCA+∠ACE=∠FCE,
∠ACE+∠BCE=∠ACB,
∴∠FCA=∠ECB.
∴△ACF∽△BCE,
∴![]() =
=![]() .
.
(3)①如图,由△ECB∽△FCA,可得:AF:BE=CF:EC=![]() .
.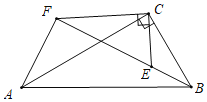
设BE=a,则AF=![]() a,
a,
∵B,E,F共线,
∴∠BEC=∠AFC=120°,
∵∠EFC=30°,
∴∠AFB=90°,
在Rt△ABF中,AB=2BC=6,AF=![]() a,BF=EF+BE=4+a,
a,BF=EF+BE=4+a,
∴(![]() a)2+(4+a)2=62,
a)2+(4+a)2=62,
∴a=-1+![]() 或-1-
或-1-![]() (舍弃),
(舍弃),
∴AF=![]() a=3
a=3![]() -
-![]()
②如图,当E,B,F共线时,同法可证:AF=![]() BE,∠AFB=90°,
BE,∠AFB=90°,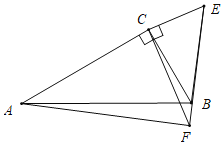
在Rt△ABF中,62=(4-a)2+(![]() a)2,
a)2,
解得a=1+![]() 或1-
或1-![]() (舍弃),
(舍弃),
∴AF=![]() a=3
a=3![]() +
+![]() .
.
AF的长为3![]() -
-![]() 或3
或3![]() +
+![]() .
.