Question

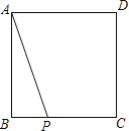
【题目】如图，正方形ABCD中，点P在BC边上，连接AP，将线段PA绕点P顺时针旋转90°得到线段PE，过点E作EF⊥BC，分别交直线BC，AC于点F，G．

（1）依题意补全图形；

（2）求证：BP=EF；

（3）连接PG，CE，用等式表示线段PG，CE，CD之间的数量关系，并证明．

Answer 1

【答案】（1）见解析；（2）见解析；（3）结论：PG2=CD2+CE2，理由见解析

【解析】

（1）根据要求画出图形即可．

（2）证明△ABP≌△PFE（AAS），即可解决问题．

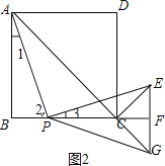
（3）证明PF为线段EG的垂直平分线，可得PE=PG，再利用勾股定理即可解决问题．

解：（1）补全的图形如图所示；

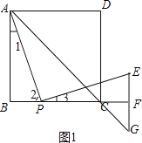
（2）证明：如图，

∵四边形ABCD是正方形，

∴∠B=90°，

∴∠1+∠2=90°，

∵线段PA绕点P顺时针旋转90°得到线段PE，

∴PA=PE，∠APE=90°，

∴∠2+∠3=90°，

∴∠1=∠3，

∵EF⊥BC于F，

∴∠EFP=90°=∠B，

在△ABP和△PFE中，

∵∠B=∠EFP，∠1=∠3，PA=PE，

∴△ABP≌△PFE（AAS），

∴BP=EF．

（3）结论：PG2=CD2+CE2．

理由：如图，

∵四边形ABCD是正方形，

∴AB=BC=CD．

∵△ABP≌△PFE，

∴AB=PF，

∴BC=PF=CD，

∴BC-PC=PF-PC，即BP=CF．

又∵BP=EF，

∴EF=CF，

∴△CEF是等腰直角三角形，EF=CE．

∵∠FCG=∠ACB=∠DCB=45°，

∴CF=FG=EF，

∴PF为线段EG的垂直平分线，

∴PE=PG．

在Rt△PFE中，有PE2=PF2+EF2，

∴PG2=CD2+CE2．