Question

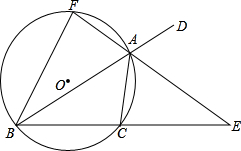
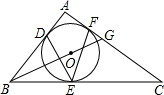
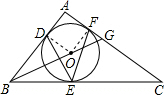
如图，⊙O是△ABC的内切圆，与AB、BC、CA分别相切于点D、E、F，∠DEF=45度．连接BO并延长交AC于点G，AB=4，AG=2．
（1）求∠A的度数；
（2）求⊙O的半径．

Answer 1

（1）连接OD，OF，
∵⊙O是△ABC的内切圆，
∴OD⊥AB，OF⊥AC，又∠DOF=2∠DEF=2×45°=90°，
∴∠ODA=∠OFA=∠DOF=90°，
∴四边形ADOF是矩形，
∴∠A=90°；

（2）设⊙O的半径为r，
由（1）知四边形ADOF是矩形，又OD=OF，
∴四边形ADOF是正方形．
∴OD∥AC．
∴△BOD∽△BGA．
∴

DO

AG

=

BD

BA

．
即

r

2

=

4-r

4

，
解得r=

4

3

．
∴⊙O的半径为

4

3

．