题目内容
规定三角形的三条内角平分线的交点叫三角形的内心.
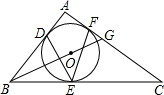
(1)已知I为三角形ABC的内心,连接AI交三角形ABC的外接圆于点D,如图所示,连接BD和CD,求证:BD=CD=ID.
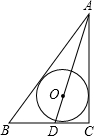
(2)己知三角形ABC,AD平分∠BAC且与它的外接圆交于点D,在线段AD上有一点I满足BD=ID.试问点I是否是三角形ABC的内心?若是加以证明;若不是,说明理由.

(1)已知I为三角形ABC的内心,连接AI交三角形ABC的外接圆于点D,如图所示,连接BD和CD,求证:BD=CD=ID.

(2)己知三角形ABC,AD平分∠BAC且与它的外接圆交于点D,在线段AD上有一点I满足BD=ID.试问点I是否是三角形ABC的内心?若是加以证明;若不是,说明理由.

(1)证明:

连接BI,
∵I是△ABC的内心,
∴∠BAD=∠DAC,∠ABI=∠CBI,
∴弧BD=弧DC,
∴BD=DC,
∵∠BID=∠ABI+∠BAD,∠IBD=∠CBI+∠DBC,
∵∠CAD=∠BAD=∠DBC,
∴∠DBI=∠BID,
∴BD=DI,
∴BD=CD=ID.
(2)答:I是三角形ABC的内心.
证明:连接BI,
∵∠BID=∠ABI+∠BAD,∠IBD=∠CBI+∠DBC,BD=ID,
∴∠BID=∠IBD,
∵AD平分∠BAC,
∴∠BAD=∠CAD=∠DBC,
∴∠ABI=∠CBI=∠BID-∠BAI,
∴∠ABI=∠CBI,
即I在∠ABC的平分线上,
即I是∠BAC何∠ABC的平分线的交点,
∴I也在∠ACB的角平分线上,
即I是三角形ABC的内心.

连接BI,
∵I是△ABC的内心,
∴∠BAD=∠DAC,∠ABI=∠CBI,
∴弧BD=弧DC,
∴BD=DC,
∵∠BID=∠ABI+∠BAD,∠IBD=∠CBI+∠DBC,
∵∠CAD=∠BAD=∠DBC,
∴∠DBI=∠BID,
∴BD=DI,
∴BD=CD=ID.
(2)答:I是三角形ABC的内心.

证明:连接BI,
∵∠BID=∠ABI+∠BAD,∠IBD=∠CBI+∠DBC,BD=ID,
∴∠BID=∠IBD,
∵AD平分∠BAC,
∴∠BAD=∠CAD=∠DBC,
∴∠ABI=∠CBI=∠BID-∠BAI,
∴∠ABI=∠CBI,
即I在∠ABC的平分线上,
即I是∠BAC何∠ABC的平分线的交点,
∴I也在∠ACB的角平分线上,
即I是三角形ABC的内心.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目