题目内容
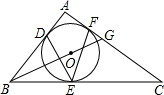
如图,⊙O是等边△ABC的外接圆,⊙O的半径为4,则等边△ABC的边长为______.


连接OB,OC,过点O作OD⊥BC于D,
∴BC=2BD,
∵⊙O是等边△ABC的外接圆,
∴∠BOC=
×360°=120°,
∵OB=OC,
∴∠OBC=∠OCB=
=
=30°,
∵⊙O的半径为4,
∴OA=4,
∴BD=OB•cos∠OBD=4×cos30°=4×
=2
,
∴BC=4
.
∴等边△ABC的边长为4
.
故答案为:4
.

∴BC=2BD,
∵⊙O是等边△ABC的外接圆,
∴∠BOC=
| 1 |
| 3 |
∵OB=OC,
∴∠OBC=∠OCB=
| 180°-∠BOC |
| 2 |
| 180°-120° |
| 2 |
∵⊙O的半径为4,
∴OA=4,
∴BD=OB•cos∠OBD=4×cos30°=4×
| ||
| 2 |
| 3 |
∴BC=4
| 3 |
∴等边△ABC的边长为4
| 3 |
故答案为:4
| 3 |


练习册系列答案
相关题目