题目内容

如图，△ABC内接于⊙O，AE是∠BAC外角∠CAD的平分线，交BC延长线于点E，延长EA交⊙O于点F，连接BF，求证：FB2=FA•FE．
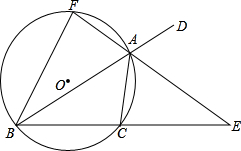
证明：∵AE是∠BAC外角∠CAD的平分线，
∴∠DAE=∠CAE，又∠DAE=∠FAB，∠FBE=∠CAE，
∴∠FBE=∠FAB，
又∵∠BFE=∠AFB
∴△FAB∽△FBE
∴FB：FA=FE：FB即FB2=FA•FE．
练习册系列答案
相关题目
如图，在△ABC中，BD是角平分线，CE是高，且∠ACB=60°，∠ADB=97°，求∠A和∠ACE的度数．
如图，在△ABC中，AE是中线，AD是角平分线，AF是高，BE=2，AF=3，填空：
（1）BE=______=
1
2
______．
（2）∠BAD=______=
1
2
______．
（3）∠AFB=______=______．
（4）S△AEC=______．
如图，已知CB、CD分别是钝角△AEC和锐角△ABC的中线，且AC=AB，给出下列结论：①AE=2AC；②CE=2CD；③∠ACD=∠BCE；④CB平分∠DCE，则以上结论正确的是（　　）
A．①②④B．①③④C．①②③D．①②③④
已知：∠MON=40°，OE平分∠MON，点A、B、C分别是射线OM、OE、ON上的动点（A、B、C不与点O重合），连接AC交射线OE于点D．设∠OAC=x°．

（1）如图1，若AB∥ON，则
①∠ABO的度数是______；
②当∠BAD=∠ABD时，x=______；当∠BAD=∠BDA时，x=______．
（2）如图2，若AB⊥OM，则是否存在这样的x的值，使得△ADB中有两个相等的角？若存在，求出x的值；若不存在，说明理由．
如图，△ABC的三边满足关系BC=
1
2
（AB+AC），O、I分别为△ABC的外心、内心，∠BAC的外角平分线交⊙O于E，AI的延长线交⊙O于D，DE交BC于H，
求证：（1）AI=BD；
（2）OI=
1
2
AE．
如图，⊙O是△ABC的内切圆，与AB、BC、CA分别相切于点D、E、F，∠DEF=45度．连接BO并延长交AC于点G，AB=4，AG=2．
（1）求∠A的度数；
（2）求⊙O的半径．
如图，点l是△ABC的内心，线段AI的延长线交△ABC外切圆于点D，交BC边于点E．
（1）求证：lD=BD．
（2）若
BE
AB
=
2
3
，lE=2，求AD的长．
已知△ABC，求作⊙O，使⊙O经过△ABC的三个顶点．（不写作法，保留作图痕迹）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网