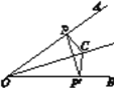题目内容
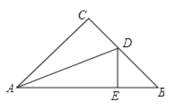
【题目】如图,现将一张矩形ABCD的纸片一角折叠,若能使点D落在AB边上F处,折痕为CE,恰好∠AEF=60°,延长EF交CB的延长线于点G. 
(1)求证:△CEG是等边三角形;
(2)若矩形的一边AD=3,求另一边AB的长.
【答案】
(1)证明:∵四边形ABCD是矩形,
∴AD∥BC即AD∥GC,
∴∠G=∠AEF=60°,
由折叠可知:∠CED=∠CEG,而∠GED=180°﹣∠AEF=120°
∴∠GEC=∠CED= ![]() ∠GED=60°即∠G=∠GEC=60°,
∠GED=60°即∠G=∠GEC=60°,
∴△CEG是等边三角形;
(2)解:∵四边形ABCD是矩形∴∠A=∠D=90°,AB=CD,
由(1)可知∠AEF=∠CED=60°,∴∠AFE=∠DCE=30°,
∴EF=2AE,CE=2DE.设AE=x,则EF=2x,ED=EF=2x,
∴AD=x+2x=3,CE=4x,解得,x=1,DE=2,CE=4,
在Rt△CDE中,CD= ![]()
∴AB=2 ![]() .
.
【解析】(1)由折叠可知∠DEC=∠FEC,已知∠AEF=60°,可知∠DEC=∠FEC=60°,由AD∥GC,可知∠G=∠AEF=60°,故有∠G=∠FEC=60°,所以△CEG是等边三角形;(2)在Rt△AEF中,∠AEF=60°,设AE=x,则EF=2x,由折叠的性质得ED=EF=2x,根据AE+ED=AD,列方程求x,在Rt△CDE中,DE=2,∠DEC=60°,可得CE=2DE=4,利用勾股定理可求CD,即AB的长.
【考点精析】解答此题的关键在于理解翻折变换(折叠问题)的相关知识,掌握折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目