题目内容
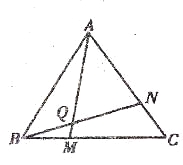
【题目】如图所示,已知C是∠AOB的平分线上一点,点P,P′分别在边OA,OB上,如果要得到OP=OP′,需要添加以下条件中的某一个,那么所有可能结果的序号为________.
①∠OCP=∠OCP′;②∠OPC=∠OP′C;③PC=P′C;④PP′⊥OC.
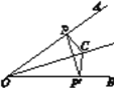
【答案】①②④
【解析】
由射线OC上的任意一点到∠AOB的两边的距离都相等,根据角平分线的判定定理可知OC平分∠AOB .要得到OP=O P′,就要让△OCP≌△OCP′,①②④都行,只有③PC=P′C 不行,因为证明三角形全等没有边边角定理.
①若①∠OCP=∠OCP′,根据ASA定理可求出△OCP≌△OCP′,由三角形全等的性质可知OP=O P′.正确;
②若∠OPC=∠OP′C,根据AAS定理可得△OCP≌△OCP′,由三角形全等的性质可知OP=O P′.正确;
③若PC=P′C 条件不能得出.错误;
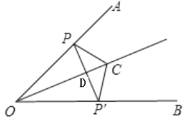
④若PP′⊥OC ,根据ASA定理可求出△OPD≌△![]() ,由三角形全等的性质可知OP=O P′.正确.
,由三角形全等的性质可知OP=O P′.正确.
故答案为①②④.

【题目】(根据市教委提出的学生每天体育锻炼不少于1小时的要求,为确保阳光体育运动时间得到落实,某校对九年级学生每天参加体育锻炼的时间作了一次抽样调查,其中部分结果记录如下:
时间分组(小时) | 频数(人数) | 频率 |
0≤t<0.5 | 10 | 0.2 |
0.5≤t<1 | 0.4 | |
1≤t<1.5 | 10 | 0.2 |
1.5≤t<2 | 0.1 | |
2≤t<2.5 | 5 | |
合计 | 1 |
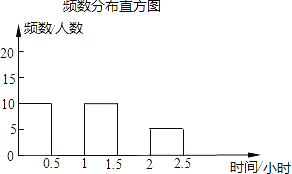
请你将频数分布表和频数分布直方图补充完整.
【题目】抛物线y=﹣x2+bx+c上部分点的横坐标x,纵坐标y的对应值如表:
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | … |
y | … | 0 | 4 | 6 | 6 | 4 | … |
从上表可知,有下列说法:
①抛物线与y轴的交点为(0,6);
②抛物线的对称轴是x=1;
③抛物线与x轴有两个交点,它们之间的距离是 ![]() ;
;
④在对称轴左侧y随x增大而增大.
其中正确的说法是( )
A.①②③
B.②③④
C.②③
D.①④