题目内容
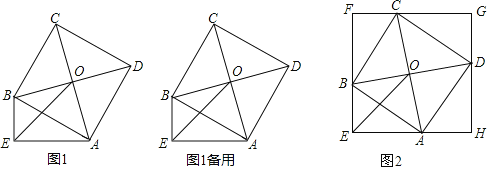
【题目】在Rt△AEB中,∠AEB=90°,以斜边AB为边向Rt△AEB形外作正方形ABCD,若正方形ABCD的对角线交于点O(如图1).
(1)求证:EO平分∠AEB;
(2)猜想线段OE与EB、EA之间的数量关系为 (直接写出结果,不要写出证明过程);
(3)过点C作CF⊥EB于F,过点D作DH⊥EA于H,CF和DH的反向延长线交于点G(如图2),求证:四边形EFGH为正方形.
【答案】(1)求证见解析;(2)![]() OE=EB+EA;(3)见解析.
OE=EB+EA;(3)见解析.
【解析】
(1)延长EA至点F,使AF=BE,连接OF,由SAS证得△OBE≌△OAF,得出OE=OF,∠BEO=∠AFO,由等腰三角形的性质与等量代换即可得出结论;
(2)判断出△EOF是等腰直角三角形,根据勾股定理即可得出结论;
(3)先根据ASA证得△ABE≌△ADH,△ABE≌△BCF,△ADH≌△DCG,△DCG≌△CBF,得出FG=EF=EH=HG,再由∠F=∠H=∠AEB=90°,由此可得出结论.
(1)证明:延长EA至点F,使AF=BE,连接OF,如图所示:
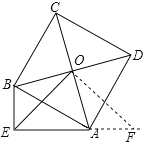
∵四边形ABCD是正方形,
∴∠BOA=90°,OB=OA,
∵∠AEB=90°,
∴∠OBE+∠OAE=360°﹣90°﹣90°=180°,
∵∠OAE+∠OAF=180°,
∴∠OBE=∠OAE,在△OBE与△OAF中,
 ,
,
∴△OBE≌△OAF(SAS),
∴OE=OF,∠BEO=∠AFO,
∴∠AEO=∠AFO,
∴∠BEO=∠AEO,
∴EO平分∠AEB;
(2)解:![]() OE=EB+EA,理由如下:
OE=EB+EA,理由如下:
由(1)得:△OBE≌△OAF,
∴OE=OF,∠BOE=∠AOF,
∵∠BOE+∠AOE=90°,
∴∠AOF+∠AOE=90°,
∴∠EOF=90°,
∴△EOF是等腰直角三角形,
∴2OE2=EF2,
∵EF=EA+AF=EA+EB,
∴2OE2=(EB+EA)2,
∴![]() OE=EB+EA,
OE=EB+EA,
故答案为:![]() OE=EB+EA;
OE=EB+EA;
(3)证明:∵CF⊥EB,DH⊥EA,
∴∠F=∠H=∠AEB=90°,
∵四边形ABCD是正方形,
∴AB=AD,∠BAD=90°,
∴∠EAB+∠DAH=90°,∠EAB+∠ABE=90°,∠ADH+∠DAH=90°,
∴∠EAB=∠HDA,∠ABE=∠DAH.
在△ABE与△ADH中,
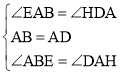 ,
,
∴△ABE≌△ADH(ASA),
∴BE=AH,AE=DH,
同理可得:△ABE≌△BCF,△ADH≌△DCG,△DCG≌△CBF,
∴BE=CF,AE=BF,AH=DG,DH=CG,DG=CF,CG=BF,
∴CG+FC=BF+BE=AE+AH=DH+DG,
∴FG=EF=EH=HG,
∵∠F=∠H=∠AEB=90°,
∴四边形EFGH为正方形.

 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案【题目】均匀的正四面体的各面依次标有![]() 四个数字
四个数字![]() 小明做了60次投掷试验,结果统计如下:
小明做了60次投掷试验,结果统计如下:
朝下数字 | 1 | 2 | 3 | 4 |
出现的次数 | 16 | 20 | 14 | 10 |
![]() 计算上述试验中“4朝下”的频率是多少?
计算上述试验中“4朝下”的频率是多少?
![]() “根据试验结果,投掷一次正四面体,出现2朝下的概率是
“根据试验结果,投掷一次正四面体,出现2朝下的概率是![]() ”的说法正确吗?为什么?
”的说法正确吗?为什么?