题目内容
【题目】如图,在直角坐标系中,矩形 ABCO 的边 OA 在 x 轴上,边 OC 在 y 轴上,点 B 的坐标为(3,4),直线 CD 分别交 OB、AB 于点 D、E,若 BD=BE,则点 D 的坐标为______.
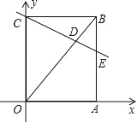
【答案】![]()
【解析】
由四边形ABCO是矩形,点B的坐标为(3,4),求得BC=OA=3,OC=AB=4,根据等腰三角形的等边对等角,等角对等边,求得点E的坐标,用待定系数法求出直线CD和直线OB 的解析式,联立方程组解出D点的坐标.
∵四边形ABCO是矩形,点B的坐标为(3,4),
∴BC=OA=3,OC=AB=4,OC∥AB,
∴C(0,4),
∵BD=BE,
∴∠BDE=∠BED,
∵OC∥AB,
∴∠OCE=∠BED,又∠CDO=∠BDE,
∴∠OCD=∠ODC,
∴OD=OC=4,
在RtΔOAB中,OA=3,AB=4,由勾股定理得
OB=![]() =5,
=5,
∴BD=BE=1,
∴E(3,3),
∴直线CE的解析式:![]() ,
,
直线OB的解析式:![]() ,
,
联立方程组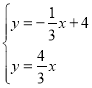 ,解得:
,解得: ,
,
∴![]() ,
,
故答案为:![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】体育课上,七年级某班男同学进行了100米测验,达标成绩为15秒,下表是梦想小组8名男生的成绩记录,其中“+”表示成绩大于15秒.
﹣0.8 | +1 | ﹣1.2 | 0 | ﹣0.7 | +0.6 | ﹣0.4 | ﹣0.1 |
问:(1)这个小组男生的达标率为多少?(达标率=![]() )
)
(2)这个小组男生的平均成绩是多少秒?
【题目】某摩托车厂本周计划每日生产450辆摩托车,由于工人实行轮休, 每日上班人数不一定相等,实际每日生产量与计划量相比情况如下表: [增加的辆数为正数,减少的辆数为负数]
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增减 | -5 | +7 | -3 | +4 | +10 | -9 | -25 |
(1)本周星期六生产多少辆摩托车?
(2)本周总产量与计划产量相比,是增加了还是减少了?为什么?
(3)产量最多的那天比产量最少的那天多生产多少辆?