题目内容
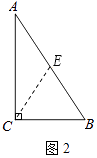
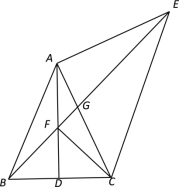
【题目】在△ABC中,AB=AC,∠BAC=50° ,D是BC的中点,以AC为腰向外作等腰直角△ACE,∠EAC=90°,连接BE,交AD于点F,交AC于点G.
(1)求∠AEB的度数;
(2)求证:∠AEB=∠ACF;
(3)若AB=4,求![]() 的值.
的值.
【答案】(1)20°;(2)32.
【解析】
(1)根据等腰直角三角形的旋转得出∠ABE=∠AEB,求出∠BAE,根据三角形内角和定理求出即可;
(2)根据等腰三角形的性质得出∠BAF=∠CAF,根据SAS推出△BAF≌△CAF,根据全等得出∠ABF=∠ACF,即可得出答案;
(3)根据全等得出BF=CF,求出∠CFG=∠EAG=90°,根据勾股定理求出EF2+BF2=EF2+CF2=EC2,EC2=AC2+AE2,即可得出答案.
(1)∵AB=AC,AC=AE.
∴AB=AE,
∴∠AEB=∠ABE.
∵∠BAC=50°,∠CAE=90°,
∴∠BAE=50°+90°=140°.
∴∠AEB=![]() .
.
(2)∵AB=AC,D是BC的中点,
∴∠BAF=∠CAF.
∴△ABF≌△ACF.
∴∠ABF=∠ACF.
∵∠AEB=∠ABE,
∴∠AEB=∠ACF.
(3)∵∠AEB=∠ACF ,∠AGE=∠CGF,
∴∠CFE=∠CAE=90°.
∴![]() .
.
∵CF=BF,
∴![]() .
.
∵![]() ,
,
∴![]() .
.

 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案【题目】某农产品生产基地收获红薯192吨,准备运给甲、乙两地的承包商进行包销.该基地用大、小两种货车共18辆恰好能一次性运完这批红薯,已知这两种货车的载重量分别为14吨/吨和8吨/辆,运往甲、乙两地的运费如下表:
车型 | 运费 | |
运往甲地/(元/辆) | 运往乙地/(元/辆) | |
大货车 | 720 | 800 |
小货车 | 500 | 650 |
(1)求这两种货车各用多少辆;
(2)如果安排10辆货车前往甲地,其余货车前往乙地,其中前往甲地的大货车为a辆,总运费为w元,求w关于a的函数关系式;
(2)在(2)的条件下,若甲地的承包商包销的红薯不少于96吨,请你设计出使总运费最低的货车调配方案,并求出最低总运费.