题目内容
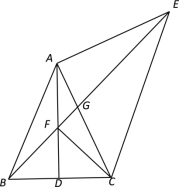
【题目】如图,在△ABC中,∠C=90°,CA=4,CB=3. ![]() 与CA延长线、AB、CB延长线相切,切点分别为E、D、F,则该弧所在圆的半径为 .
与CA延长线、AB、CB延长线相切,切点分别为E、D、F,则该弧所在圆的半径为 . 
【答案】6
【解析】解: 在Rt△ACB中,∠C=90°,AC=,BC=3,由勾股定理得:AB=5,
设弧所在的圆的圆心为O,圆的半径为r,连接OE、OF,如图,
∵. ![]() 与CA延长线、AB、CB延长线相切,切点分别为E、D、F,
与CA延长线、AB、CB延长线相切,切点分别为E、D、F,
∴AE=AD,BF=BD,∠OEC=∠OFC=90°,
∵∠C=90°,OE=OF=r,
∴四边形CEOF是正方形,
∴CE=CF=OE=OF=r,
则AE=AD=r﹣4,BF=DB=r﹣3,
∴r﹣3+r﹣4=5,
解得:r=6,
所以答案是:6.
【考点精析】认真审题,首先需要了解勾股定理的概念(直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2),还要掌握切线的性质定理(切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径)的相关知识才是答题的关键.

练习册系列答案
相关题目