题目内容
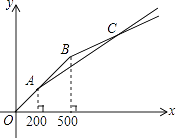
【题目】一列快车和一列慢车同时从甲地出发,分别以速度v1、v2(单位:km/h,且v1>2v2)匀速驶向乙地.快车到达乙地后停留了2h,沿原路仍以速度v1匀速返回甲地.设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示从慢车出发至慢车到达乙地的过程中,y与x之间的函数关系.根据图象进行以下探究: 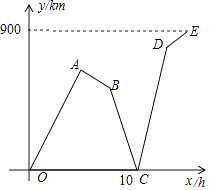
(1)甲、乙两地之间的距离为km;
(2)求线段AB、CD所表示的y与x之间的函数表达式;
(3)慢车出发多长时间后,两车相距480km?
【答案】
(1)900
(2)解:根据图象,得慢车的速度为 ![]() =60(km/h),
=60(km/h),
快车的速度为 ![]() =150(km/h),
=150(km/h),
所以线段AB所表示的y与x之间的函数表达式为y1=900﹣60x,
所以线段CD所表示的y与x之间的函数表达式为
y2=(60+150)(x﹣10)=210x﹣2100;
(3)解:①线段OA所表示的y与x之间的函数表达式为y3=90x(0≤x<6),
令y3=480,得x= ![]() ,
,
②线段AB所表示的y与x之间的函数表达式为y1=﹣60x+900(6≤x<8),
令y1=480,得x=7,
③线段CD所表示的y与x之间的函数表达式为y2=210x﹣2100(10≤x<14),
令y2=480,得x= ![]() .
.
答:慢车出发 ![]() h、7h、
h、7h、 ![]() h后,两车相距480km.
h后,两车相距480km.
【解析】(1)由图象即可得到结论;(2)根据图象,得到慢车的速度为 ![]() =60(km/h),快车的速度为
=60(km/h),快车的速度为 ![]() =150(km/h),于是得到结论;(3)根据每段的函数解析式即可得到结论.
=150(km/h),于是得到结论;(3)根据每段的函数解析式即可得到结论.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目