题目内容
【题目】(1)根据下列叙述填依据:
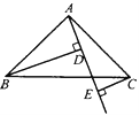
已知:如图①,AB∥CD,∠B+∠BFE=180°,求∠B+∠BFD+∠D的度数.
解:因为∠B+∠BFE=180°,
所以AB∥EF( ).
又因为AB∥CD,
所以CD∥EF( ).
所以∠CDF+∠DFE=180°( ).
所以∠B+∠BFD+∠D=∠B+∠BFE+∠DFE+∠D=360°.
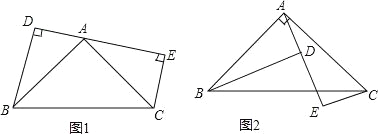
(2)根据以上解答进行探索:如图②,AB∥EF,∠BDF与∠B,∠F有何数量关系?并说明理由.
(3)如图③④,AB∥EF,你能探索出图③、图④两个图形中,∠BDF与∠B,∠F的数量关系吗?请直接写出结果.

【答案】(1)(1)同旁内角互补,两直线平行;平行于同一直线的两条直线互相平行;两直线平行,同旁内角互补;(2)∠BDF=∠B+∠F,理由见解析;(3)∠BDF=∠F-∠B.
【解析】试题分析:(1)根据平行线的性质和判定填空即可;
(2)过点D作AB的平行线DC,根据两直线平行,内错角相等证明即可;
(3)与(2)的证明方法类似,可以求出![]() 与
与![]() 的数量关系.
的数量关系.
试题解析:因为![]()
所以AB∥EF(同旁内角互补,两直线平行),
因为AB∥CD(已知),
所以CD∥EF(如果两条直线都与第三条直线平行,那么这两条直线也平行),
所以![]() (两直线平行,同旁内角互补),
(两直线平行,同旁内角互补),
所以![]()
(2)过点D作AB的平行线DC,

因为AB∥EF,
所以∠B=∠BDC,
因为AB∥EF,
所以CD∥EF,
所以∠F=∠FDC,
所以∠BDF=∠B+∠F
(3)过点D作AB的平行线DC,
根据平行线的性质可以证明图③∠BDF+∠B=∠F;图④∠BDF+∠B=∠F.

练习册系列答案
相关题目