题目内容
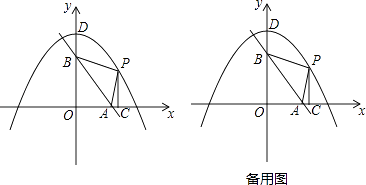
【题目】如图1,在平行四边形ABCD中,E,F分别在边AD,AB上,连接CE,CF,且满足∠DCE=∠BCF,BF=DE,∠A=60°,连接EF.
(1)若EF=2,求△AEF的面积;
(2)如图2,取CE的中点P,连接DP,PF,DF,求证:DP⊥PF.

【答案】(1)![]() (2)证明见解析
(2)证明见解析
【解析】分析:(1)先证明△CDE≌△CBF,得到CD=CB,可得ABCD是菱形,则AD=AB,由DE=BF得AE=AF,则△AEF是等边三角形,根据EF的长可得△AEF的面积;
(2)延长DP交BC于N,连结FN,证明△CPN≌△EPD,得到AE=BN,证明△FBN≌△DEF,得到FN=FD,根据等腰三角形三线合一的性质可得结论.
详解:(1)∵四边形ABCD是平行四边形,
∴∠D=∠B,
∵BF=DE,∠DCE=∠BCF,
∴△CDE≌△CBF(AAS),
∴CD=CB,
∴ABCD是菱形,
∴AD=AB,
∴AD﹣DE=AB﹣BF,即AE=AF,
∵∠A=60°,
∴△AEF是等边三角形,
∵EF=2,
∴S△AEF=![]() ×22=
×22=![]() ;
;
(2)证明:如图2,延长DP交BC于N,连结FN,

∵四边形ABCD是菱形,
∴AD∥BC,
∴∠EDP=∠PNC,∠DEP=∠PCN,
∵点P是CE的中点,
∴CP=EP.
∴△CPN≌△EPD,
∴DE=CN,PD=PN.
又∵AD=BC.
∴AD﹣DE=BC﹣CN,即AE=BN.
∵△AEF是等边三角形,
∴∠AEF=60°,EF=AE.
∴∠DEF=120°,EF=BN.
∵AD∥BC,
∴∠A+∠ABC=180°,
又∵∠A=60°,
∴∠ABC=120°,
∴∠ABC=∠DEF.
又∵DE=BF,BN=EF.
∴△FBN≌△DEF,
∴DF=NF,
∵PD=PN,
∴PF⊥PD.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目