题目内容
【题目】已知:两个等腰直角三角形(![]() )边长分别为a和b(
)边长分别为a和b(![]() )如图放置在一起,连接AD,
)如图放置在一起,连接AD,

(1)求阴影部分(![]() )的面积
)的面积
(2)如果有一个![]() 点正好位于线段
点正好位于线段![]() 的中点,连接
的中点,连接![]() .
.![]() 得到
得到![]() ,求
,求![]() 的面积
的面积
(3)(2)中的三角形![]() 比(1)中的
比(1)中的![]() 面积大还是小,大(小)多少?
面积大还是小,大(小)多少?
【答案】(1)ab;(2)(![]() a+
a+![]() b)2;(3)S△ADP大,大(
b)2;(3)S△ADP大,大(![]() a-
a-![]() b)2.
b)2.
【解析】
(1)先根据梯形的定义证明四边形ACED是梯形,再利用S阴影=S梯形-S△ACB-S△DEB即可求面积;
(2)利用S△ADP=S梯形-S△ACP-S△DEP可求面积;
(3)由于a<b,易求(a-b)2>0,即可得![]() (a2+b2)-ab>0,从而易求S△ADP>S△ABD.
(a2+b2)-ab>0,从而易求S△ADP>S△ABD.
解:(1)如图所示,
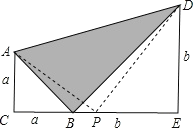
∵△ACB和△BED是等腰直角三角形,
∴∠C=∠E=90°,
∴∠C+∠E=180°,
∴AC∥DE,
∵a<b,
∴四边形ACED是梯形,
∴S阴影=S梯形-S△ACB-S△DEB
=![]() (a+b)(a+b)-
(a+b)(a+b)-![]() a2-
a2-![]() b2
b2
=ab;
(2)同(1)一样,
S△ADP=S梯形-S△ACP-S△DEP
=![]() (a+b)(a+b)-
(a+b)(a+b)-![]() ×
×![]() (a+b)a-
(a+b)a-![]() ×
×![]() (a+b)b
(a+b)b
=(![]() a+
a+![]() b)2;
b)2;
(3)S△ADP-S△ABD
=(![]() a+
a+![]() b)2-ab
b)2-ab
=(![]() a-
a-![]() b)2
b)2
∵a<b,
∴(![]() a-
a-![]() b)2>0,
b)2>0,
∴S△ADP>S△ABD.
故答案为:(1)ab;(2)(![]() a+
a+![]() b)2;(3)S△ADP大,大(
b)2;(3)S△ADP大,大(![]() a-
a-![]() b)2.
b)2.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目











