Question

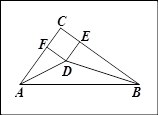
已知：如图，AB是⊙O的直径，C是⊙O上一点，OD⊥AC于点D，过点C作⊙O 的切线， 交OD的延长线与点E，连接AE.

（1）求证：AE与⊙O相切；
（2）连接BD并延长交AE于点F，若EC∥AB，OA=6，求AF的长．

Answer 1

（1）连接OC，根据切线的性质可得∠OCE=90°，由OA=OC，OD⊥AC可得∠COE=∠AOE，即可证得△COE≌△AOE，则可得∠OAE =∠OCE = 90°，从而证得结论；（2）4

试题分析：（1）连接OC，根据切线的性质可得∠OCE=90°，由OA=OC，OD⊥AC可得∠COE=∠AOE，即可证得△COE≌△AOE，则可得∠OAE =∠OCE = 90°，从而证得结论；
（2）设BF与OC相交于点G，先证得四边形OAEC是矩形，再结合OA=OC可得矩形OAEC是正方形，则可得OG∥AE，AE=AO=6，OD=ED，所以有，则可得OG=EF，由OG∥AE可得，即可得到，从而求得结果.
（1）连接OC

∵CE是⊙O的切线
∴∠OCE=90°
∵OA=OC，OD⊥AC
∴∠COE=∠AOE
∵OA=OC，∠COE=∠AOE，OE=OE
∴△COE≌△AOE(SAS)
∴∠OAE=∠OCE=90°
∴OA⊥AE
∴AE与⊙O相切；
（2）设BF与OC相交于点G
∵EC∥AB
∴∠AEC=∠OAE=90°
∵∠AEC=∠OAE=∠OCE=90°
∴四边形OAEC是矩形
∵OA=OC
∴矩形OAEC是正方形
∴OG∥AE，AE=AO=6，OD=ED
∵OG∥AE
∴
∴OG=EF
∵OG∥AE
∴
∴
∴.
点评：此类问题综合性强，难度较大，在中考中比较常见，一般作为压轴题，题目比较典型．