Question

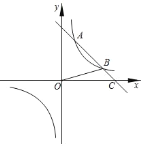
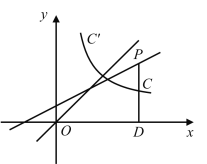
【题目】如图，过直线上一点作轴于点，线段交函数的图像于点，点为线段的中点，点关于直线的对称点的坐标为．

（1）求、的值；

（2）求直线与函数图像的交点坐标；

（3）直接写出不等式的解集．

Answer 1

【答案】（1）3，；（2）（2，）；（3）0＜x＜

【解析】

（1）根据点C′在反比例函数图像上求出m值，利用对称性求出点C的坐标，从而得出点P坐标，代入一次函数表达式求出k值；

（2）将两个函数表达式联立，得到一元二次方程，求解即可；

（3）根据（2）中交点坐标，结合图像得出结果.

解：（1）∵C′的坐标为(1，3)，

代入中，

得：m=1×3=3，

∵C和C′关于直线y=x对称，

∴点C的坐标为（3，1），

∵点C为PD中点，

∴点P（3，2），

将点P代入，

∴解得：k=；

∴k和m的值分别为：3，；

（2）联立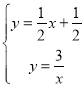：，得：，

解得：，（舍），

∴直线与函数图像的交点坐标为（2，）；

（3）∵两个函数的交点为：（2，），

由图像可知：当0＜x＜时，反比例函数图像在一次函数图像上面，

∴不等式的解集为：0＜x＜.